Two sources of sound and produce sound waves of same frequency . A listener is moving from source towards with a constant speed and he hears beats/s. The velocity of sound is . Then, equals :
The correct Answer is:A
To solve the problem, we will use the concept of apparent frequency and the beat frequency produced when two sound waves of slightly different frequencies interfere with each other.
1. Identify the Given Data:
- Frequency of both sources, f=660Hz
- Velocity of sound, v=330m/s
- Beat frequency, fb=10beats/s
- Speed of the listener, um/s (to be determined)
2. Apparent Frequency from Source S1:
The listener is moving away from source S1. The formula for the apparent frequency f1 when the observer is moving away from the source is:
f1=f(v−uv)
3. Apparent Frequency from Source S2:
The listener is moving towards source S2. The formula for the apparent frequency f2 when the observer is moving towards the source is:
f2=f(v+uv)
4. Beat Frequency Relationship:
The beat frequency is given by the difference in the apparent frequencies:
fb=|f2−f1|=10
Substituting the expressions for f1 and f2:
|f(v+uv)−f(v−uv)|=10
5. Simplifying the Equation:
Factoring out f:
f((v+u)−(v−u)v)=10
This simplifies to:
f(2uv)=10
6. Substituting Known Values:
Substitute f=660Hz and v=330m/s:
660(2u330)=10
7. Solving for u:
Rearranging gives:
1320u330=10
Simplifying:
4u=10⟹u=104=2.5m/s
Final Answer:
The speed of the listener u is 2.5m/s.
---
- Frequency of both sources, f=660Hz
- Velocity of sound, v=330m/s
- Beat frequency, fb=10beats/s
- Speed of the listener, um/s (to be determined)
The listener is moving away from source S1. The formula for the apparent frequency f1 when the observer is moving away from the source is:
f1=f(v−uv)
The listener is moving towards source S2. The formula for the apparent frequency f2 when the observer is moving towards the source is:
f2=f(v+uv)
The beat frequency is given by the difference in the apparent frequencies:
fb=|f2−f1|=10
Substituting the expressions for f1 and f2:
|f(v+uv)−f(v−uv)|=10
Factoring out f:
f((v+u)−(v−u)v)=10
This simplifies to:
f(2uv)=10
Substitute f=660Hz and v=330m/s:
660(2u330)=10
Rearranging gives:
1320u330=10
Simplifying:
4u=10⟹u=104=2.5m/s
The speed of the listener u is 2.5m/s.
Topper's Solved these Questions
Similar Questions
Two sources A and B are sounding notes of frequency 660 Hz. A listener moves from A to B with a constant velocity u. If the speed is 330 m/s , what must be the value of u so that he hears 8 beats per second ?
View SolutionTwo sources A and B are sounding notes of frequency 680 Hz. A listener moves from A to B with a constant velocity u. If the speed of sound is 340 m/s, What must be the value of u so that he hears 10 beats per second?
View SolutionA siren emitting sound of frequency 800Hz is going away from a static listener with a speed of 30 m/s. Frequency of the sound to be heard by the listener is ( Take velocity of sound as 300 m/s )
View SolutionA source is moving towards an observer with a speed of 20 m / s and having frequency of 240 Hz . The observer is now moving towards the source with a speed of 20 m / s . Apparent frequency heard by observer, if velocity of sound is 340 m / s , is
View SolutionTwo sound waves of wavelength 1m and 1.01m in a gas produce 10 beats in 3s. The velocity of sound in the gas is
View Solution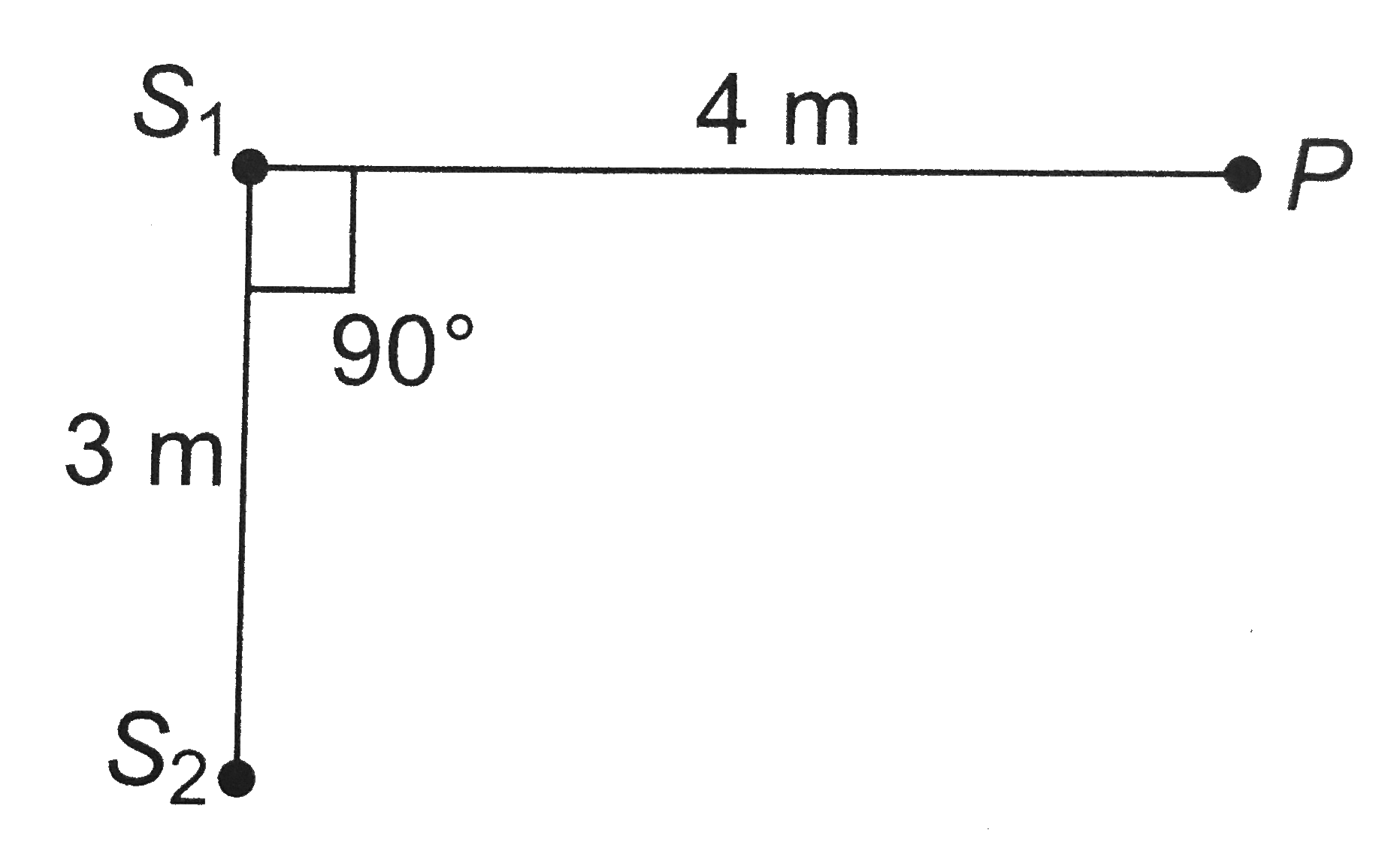
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P is
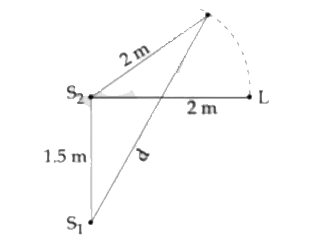
View SolutionTwo coherenet source of sound S1 and S2 produce sound waves of the same wavelength λ=1 m , in phase , S1 and S2 are placed 1.5 m a part ( see fig). A listener , loacted at L , directly in fornt of S2 finds that the intensity is at a minimum when he is 2 m away form S2. The listener moves aways form S1 keeping his distance for S2 fixed . The adjacent maximum of inesity is observed when the listener is at a distane d from S1 . Then d is
View SolutionA and B are two identical sound sources cachemitting a note of frequency 1000 Hz. A person moves from A to B along the line joining the two sources. How fast should be move to that he has 7 beats per second. velocity of sound 330 m/s ?
View SolutionA car blowing a horn of frequency 350 Hz is moving normally towards a wall a speed of 5 m/s The beat frequency heard by a person standing between the car and wall is (speed of sound in air =350 m/s )
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View Solution
