Two spheres a and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v/2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction
same as that of B
opposite to that of B
θ=tan−1(12) to the x-axis
θ=tan−1(−12) to the x-axis
The correct Answer is:D
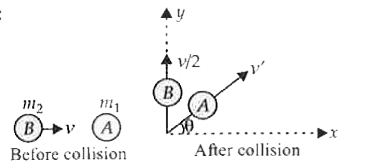
According to law of conservation of linear momentum along x - axis, we get
m1×0+m1×v=m1v.cosθ, or cosθ=m2vm1v. …(i)
According to law of conservation of linear momentum along y-axis , we get
m1×0+m2×0=m1v.sinθ+m2v2,sinθ=−m2v2m1v. ...(ii)
Divide (ii) by (i), we get
tanθ=−12 or θ=tan−1(−12) to the x-axis .
Topper's Solved these Questions
Similar Questions
Two sphere AandB of masses m1andm2 respectivelly colides. A is at rest initally and B is moving with velocity v along x-axis. After collision B has a velocity v2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
View SolutionTwo spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision, B has a velocity v2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction
View Solution
Knowledge Check
- Question 1 - Select One
Two sphere AandB of masses m1andm2 respectivelly colides. A is at rest initally and B is moving with velocity v along x-axis. After collision B has a velocity v2 in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
Aθ=tan−1(−1/2) to the x axisBsame as that of BCopposite to that of BDθ=tan−1(1/2) to the x axis - Question 2 - Select One
Two spheres A and B of masses m1andm2 respectively collide. A is at rest initially and B is moving with velocity v along x-axis. After collision B has a velocity v2direction perpendicular to the original direction. The mass A moves after collision in the direction
Asame as that of BBopposite to that of BCθ=tan−1(12) to the axisDθ=tan−1(−12) to the x-axis - Question 3 - Select One
A mass m moves with a velocity v and collides inelastically with another identical mass. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision
AvB√3vC2√3vDv√3
Two spherical balls of masses m1 and m2 collide as shown in figure. After collision mass m1 moves with velocity u/3 in a direction perpendicular to original direction. The angle θ at which mass m2 will move after collision is
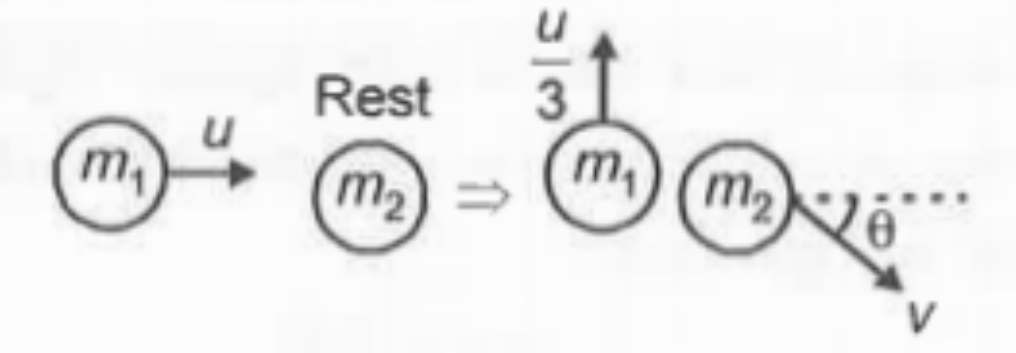 View Solution
View SolutionTwo spherical balls of masses m1 and m2 collide as shown in figure. After collision mass m1 moves with velocity u/3 in a direction perpendicular to original direction. The angle θ at which mass m2 will move after collision is
View SolutionA mass m moves with a velocity v and collides inelastically with another identical mass. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision
View SolutionA sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
View SolutionA sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
View Solution

