A sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
v
v√5
2√3v
v√3
The correct Answer is:B
To solve the problem, we will use the principle of conservation of momentum. The steps are as follows:
Step 1: Define the initial conditions
- Let sphere A have mass m and an initial velocity of 2v in the horizontal direction.
- Let sphere B also have mass m and be initially at rest, so its initial velocity is 0.
Step 2: Set up the momentum conservation equations
Since the collision is inelastic, we can apply the conservation of momentum in both the x and y directions.
In the x-direction:
- Initial momentum of sphere A: m⋅2v
- Initial momentum of sphere B: 0
- Final momentum of sphere A (after the collision): m⋅0 (since it moves vertically)
- Final momentum of sphere B: m⋅vBcosθ
Setting up the equation:
m⋅2v+0=0+m⋅vBcosθ
This simplifies to:
2v=vBcosθ(Equation 1)
In the y-direction:
- Initial momentum of sphere A: 0
- Initial momentum of sphere B: 0
- Final momentum of sphere A: m⋅v (moving vertically)
- Final momentum of sphere B: −m⋅vBsinθ (downward)
Setting up the equation:
0+0=m⋅v−m⋅vBsinθ
This simplifies to:
0=m⋅v−m⋅vBsinθ
Rearranging gives:
vBsinθ=v(Equation 2)
Step 3: Solve the equations
Now we have two equations:
1. vBcosθ=2v
2. vBsinθ=v
We can square both equations and add them:
(vBcosθ)2+(vBsinθ)2=(2v)2+v2
This gives:
v2B(cos2θ+sin2θ)=4v2+v2
Using the identity cos2θ+sin2θ=1:
v2B=5v2
Taking the square root:
vB=√5v
Conclusion
The speed of the second sphere after the collision is √5v.
---
- Let sphere A have mass m and an initial velocity of 2v in the horizontal direction.
- Let sphere B also have mass m and be initially at rest, so its initial velocity is 0.
Since the collision is inelastic, we can apply the conservation of momentum in both the x and y directions.
- Initial momentum of sphere A: m⋅2v
- Initial momentum of sphere B: 0
- Final momentum of sphere A (after the collision): m⋅0 (since it moves vertically)
- Final momentum of sphere B: m⋅vBcosθ
m⋅2v+0=0+m⋅vBcosθ
This simplifies to:
2v=vBcosθ(Equation 1)
- Initial momentum of sphere A: 0
- Initial momentum of sphere B: 0
- Final momentum of sphere A: m⋅v (moving vertically)
- Final momentum of sphere B: −m⋅vBsinθ (downward)
0+0=m⋅v−m⋅vBsinθ
This simplifies to:
0=m⋅v−m⋅vBsinθ
Rearranging gives:
vBsinθ=v(Equation 2)
Now we have two equations:
1. vBcosθ=2v
2. vBsinθ=v
(vBcosθ)2+(vBsinθ)2=(2v)2+v2
This gives:
v2B(cos2θ+sin2θ)=4v2+v2
Using the identity cos2θ+sin2θ=1:
v2B=5v2
Taking the square root:
vB=√5v
The speed of the second sphere after the collision is √5v.
Topper's Solved these Questions
Similar Questions
A particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View Solution
Knowledge Check
A mass m moves with a velocity v and collides inelastically with another identical mass. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision
AvB√3vC2√3vDv√3A mass ‘m’ moves with a velocity ‘v’ and collides inelastically with another identical mass at rest. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision :
AvB√3vC2√3 vDv√3A mass m moves with a velocity v and collides inelastically with another identical mass at rest. After collision, the first mass moves with velocity v√3 in a direction perpendicular to Before collision the initial direction of motion. The speed of the 2nd mass after collision
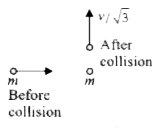 A2v√3Bv√3CvD√3v
A2v√3Bv√3CvD√3v
A smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is
View SolutionA smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is
View SolutionA ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
View SolutionA ball of mass m moving with velocity v collides elastically with another ball of identical mass coming from the opposite direction with velocity 2v. Their velocities after collisions are-
View SolutionA ball of mass 1 kg moving with a velocity of 0.4 ms−1 collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms1 in a direction making an angle of 90∘ with its initial direction. The momentum of the second ball after the collision will be (in kg ms−1)
View Solution
