Two spheres one of mass M has radius R. Another sphere has mass 4M and radius 2R. The centre to centre distance between them is 12R. Find the distance from the centre of smaller sphere where
(a) net gravitational field is zero,
(b) net gravitational potential is half the potential on the surface of larger sphere.
The correct Answer is:A, B, D
GMr2=G(4M)(12R−r)2
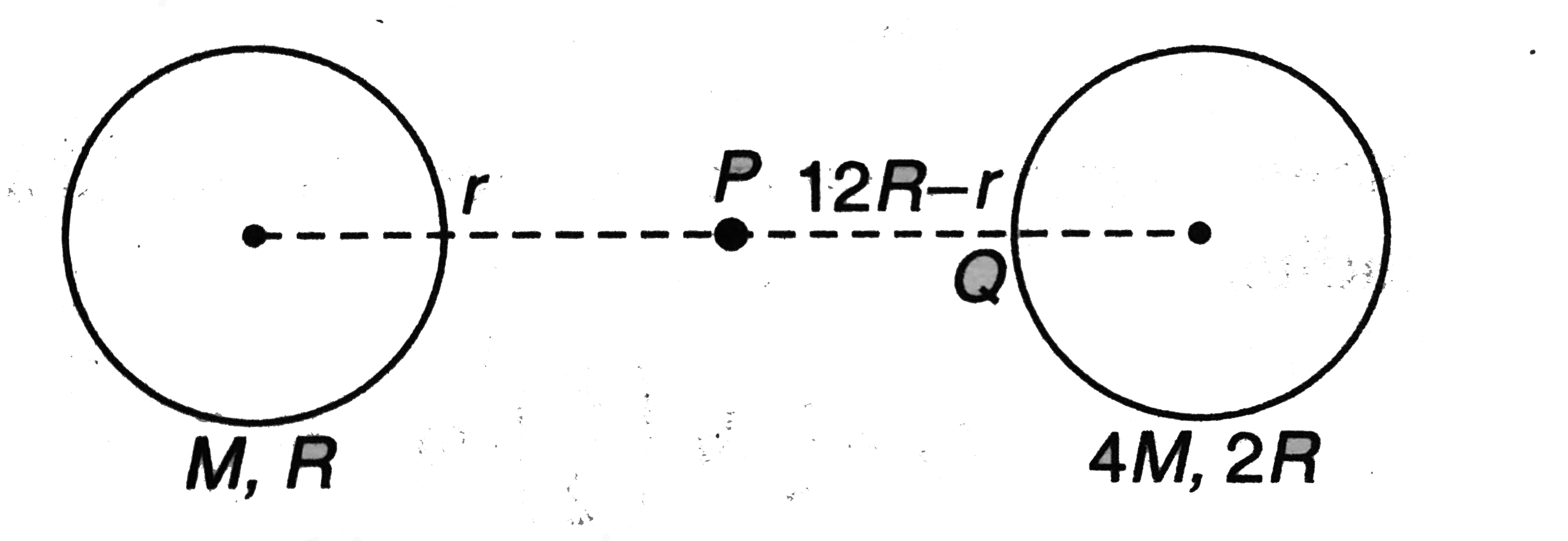
Solving this equations, we get r=4R
νP=νQ2
∴(−GMr)=[−G(4m)12R−r]
=−G(4m)2R−GM10R
solving this equation, we get
r=7.65R and 1.49R
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 Single Correct
22 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 1 Single Correct
27 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
The earth is a homogeneous sphere of mass M and radius R. There is another spherical planet of mass M and radius R whose density changes with distance r from the centre as p=p0r. (a) Find the ratio of acceleration due to gravity on the surface of the earth and that on the surface of the planet. (b) Find p0.
View SolutionA uniform rig of mas m and radius a is placed directly above a uniform sphre of mass M and of equyal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational foerce exerted by the sphere on the ring.
View Solution
Knowledge Check
P is a point at a distance r from the centre of a spherical shell of mass M and radius a, where r<a. The gravitational potential at P is
A−GMrB−GMaC−GMra2D−GM(a−ra2)The figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of these
Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of theseP is a point at a distance r from the centre of a solid sphere of radius a. The gravitational potential at P is V. IF V is plotted as a function of r, which is the correct curve ?
A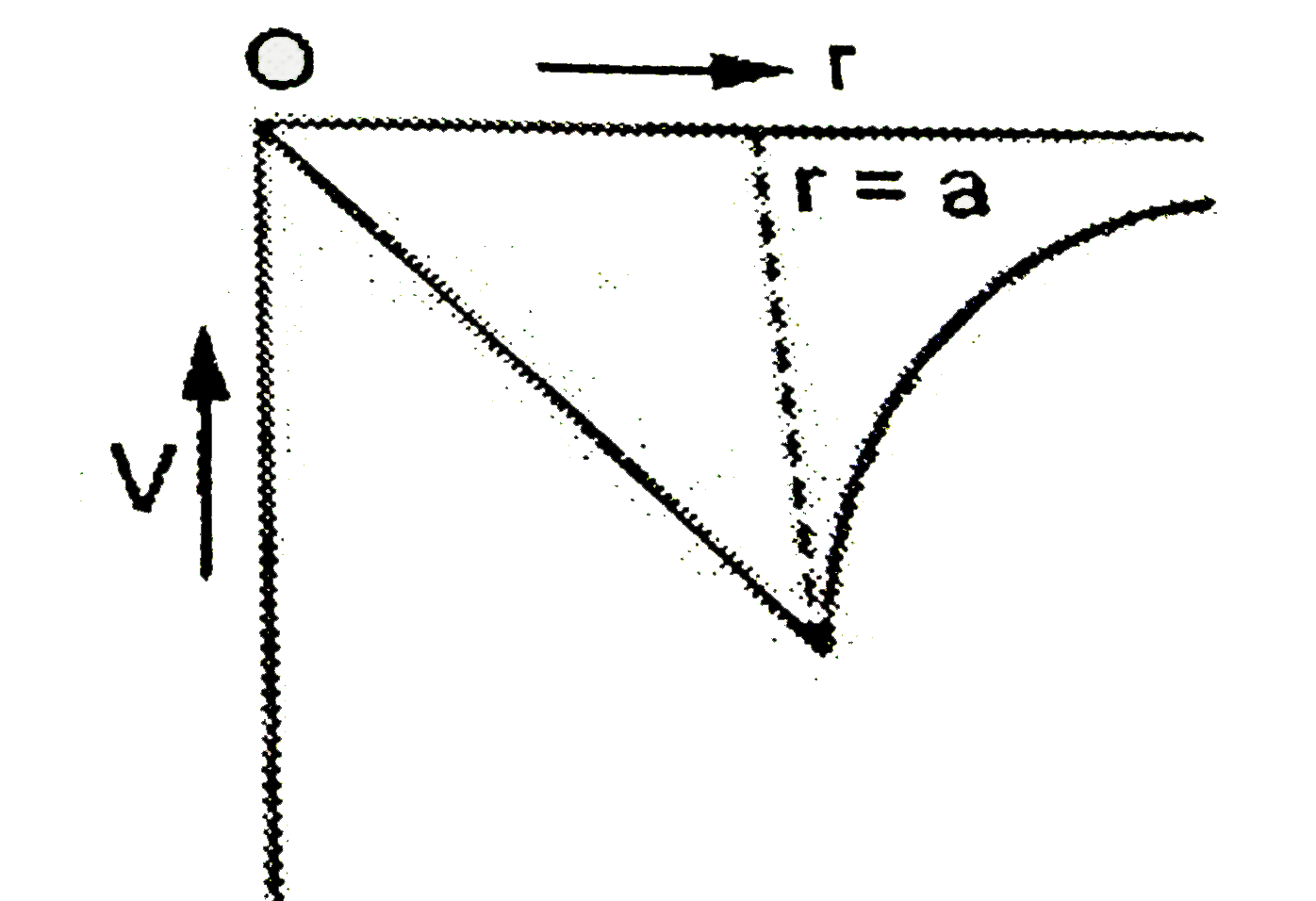 B
B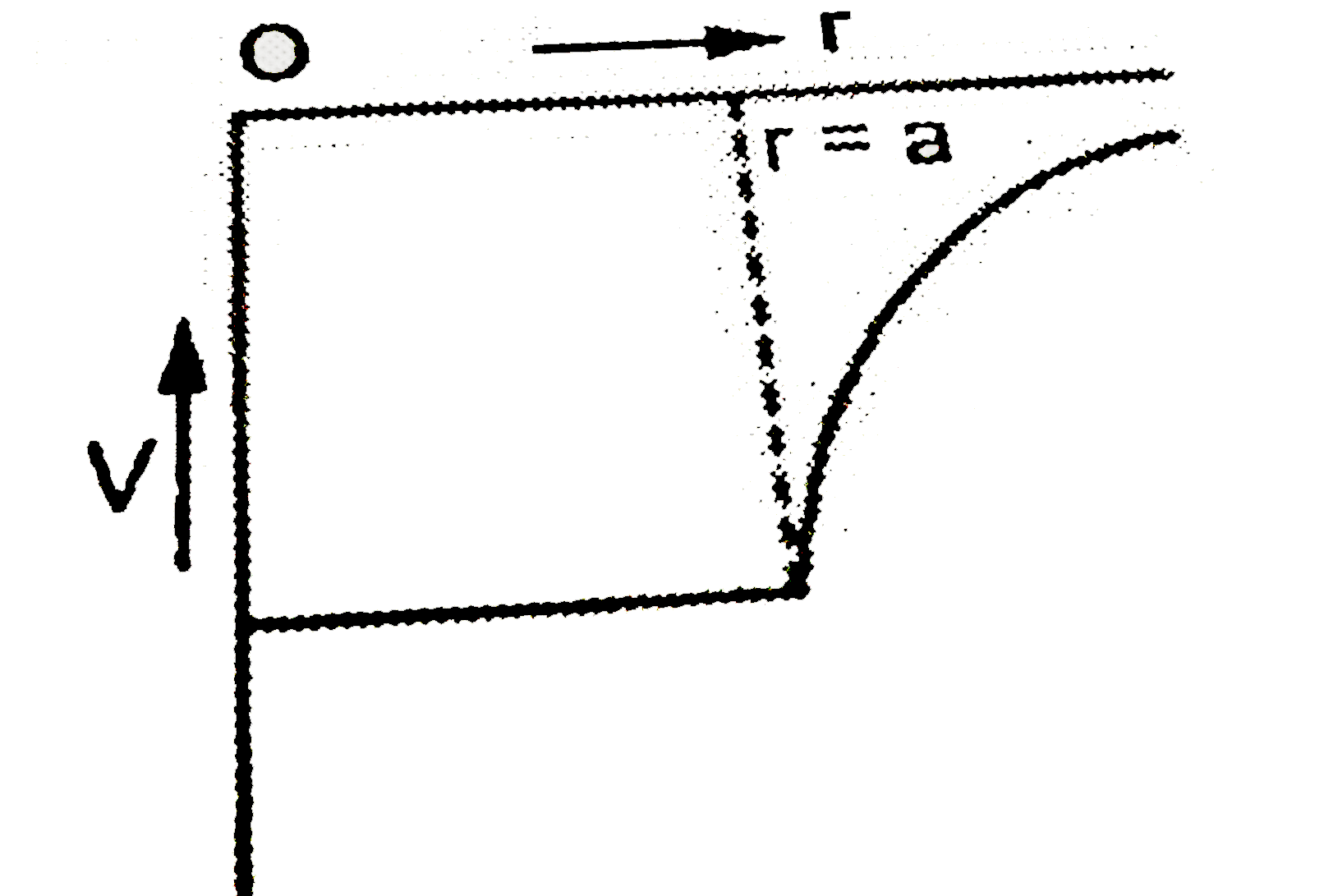 C
C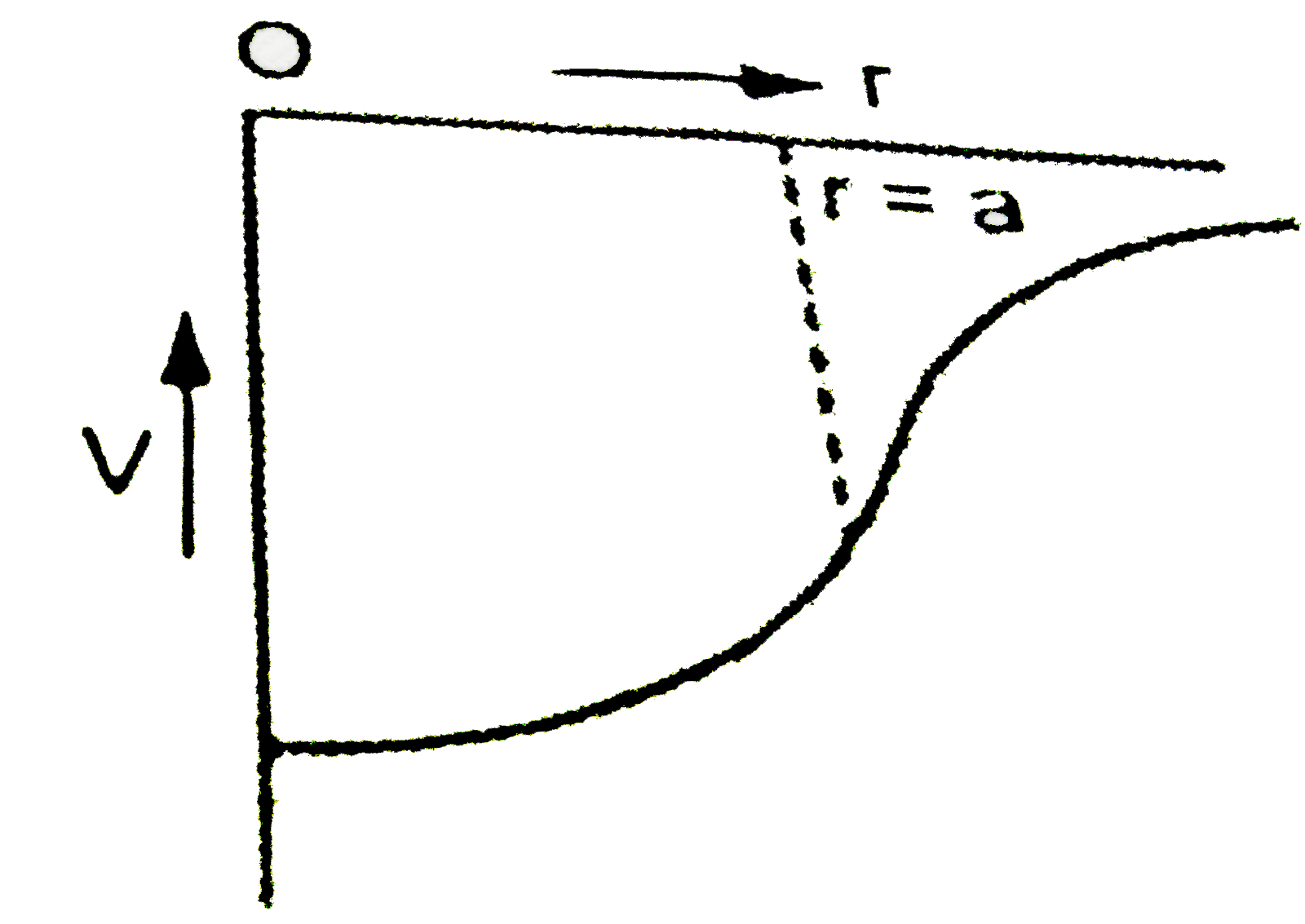 D
D
Consider a system of two spheres of masses 5 kg and 25 kg. The distance between their centres is 1.2 m. What is the distance of their centre of mass from the centre of the sphere of mass 5 g?
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionTwo heavy spheres of mass m are kept separated by a distance 2r. The gravitational field and potential at the midpoint of the line joining the centres of the spheres are
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
View SolutionA uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
View Solution
