Two spherical planets P and Q have the same uniform density $ρ,$ masses $M_{p} and M_{Q}$ and surface areas A and 4A respectively. A spherical planet R also has uniform density $ρ$ and its mass is $(M_{P} + M_{Q}) .$ The escape velocities from the plantes P,Q and R are $V_{P} V_{Q} and V_{R}$ respectively. Then

$V_{Q} > V_{R} > V_{P}$

$V_{R} > V_{R} > V_{P}$

$V_{R} / V_{P} = 3$

$V_{P} / V_{Q} = \frac{1}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

The escape velocities of the two planets, of densities $ρ_{1}$ and $ρ_{2}$ and having same radius, are $v_{1}$ and $v_{2}$ respectively. Then
A $\frac{v_{1}}{v_{2}} = \frac{ρ_{1}}{ρ_{2}}$
B $\frac{v_{2}}{v_{1}} = \frac{ρ_{2}}{ρ_{1}}$
C $\frac{v_{1}}{v_{2}} = {(\frac{ρ_{1}}{ρ_{2}})}^{2}$
D $\frac{v_{1}}{v_{2}} = \sqrt{\frac{ρ_{1}}{ρ_{2}}}$
The masses of two spherical planets A and B are $M_{A}$ and $M_{B}$ , surface areas are S and 9 S respectively. The mass of a spherical planet C is $(M_{A} + M_{B})$ . If the densities of all the planets A, B, C are same, then the escape velocities $V_{A}$ , $V_{B}$ , $V_{C}$ from the surface of these planets follow:
A $V_{C}$ gt $V_{B}$ gt $V_{A}$
B $V_{B}$ = 3 $V_{A}$
C $V_{C}$ lt $V_{B}$ lt $V_{A}$
D $V_{C}$ gt $V_{B}$ lt $V_{A}$
Three particales $P, Q$ and $R$ are placedd as per given Masses of $P, Q$ and $R$ are $\sqrt{3} m \sqrt{3} m$ and m respectively The gravitational force on a fourth particle 'S' of mass m is equal to
.
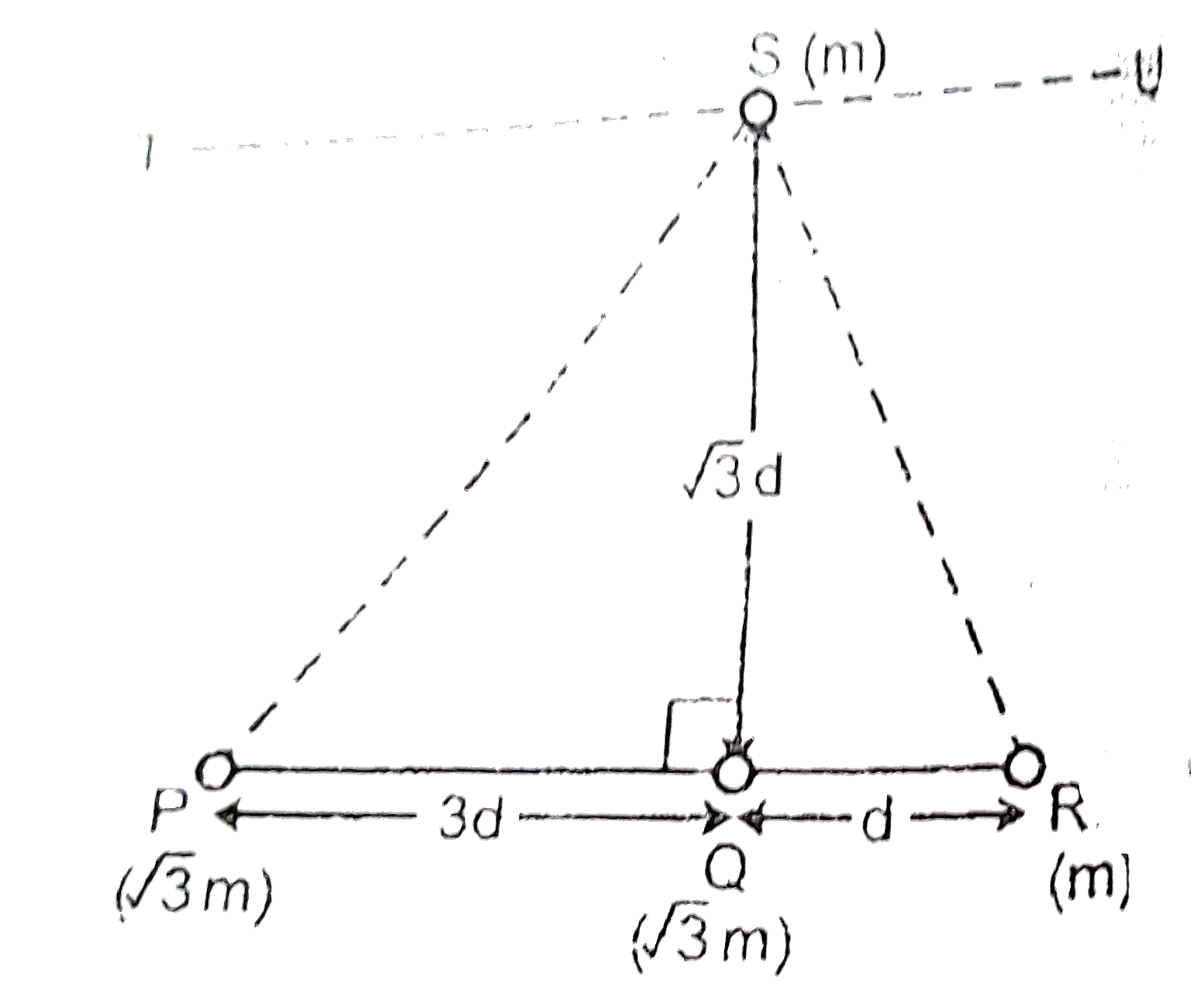A $\frac{\sqrt{3} G M^{2}}{2 d^{2}}$ in ST direction only
B $\frac{\sqrt{3} G M^{2}}{2 d^{2}}$ in SQ direction and $\frac{\sqrt{3} G M^{2}}{2 d^{2}}$ in SU direction
C $\frac{\sqrt{3} G M^{2}}{2 d^{2}}$ in SQ directiononly
D $\frac{\sqrt{3} G M^{2}}{2 d^{2}}$ in SQ direction and $\frac{\sqrt{3} G M^{2}}{2 d^{2}}$ in ST direction .