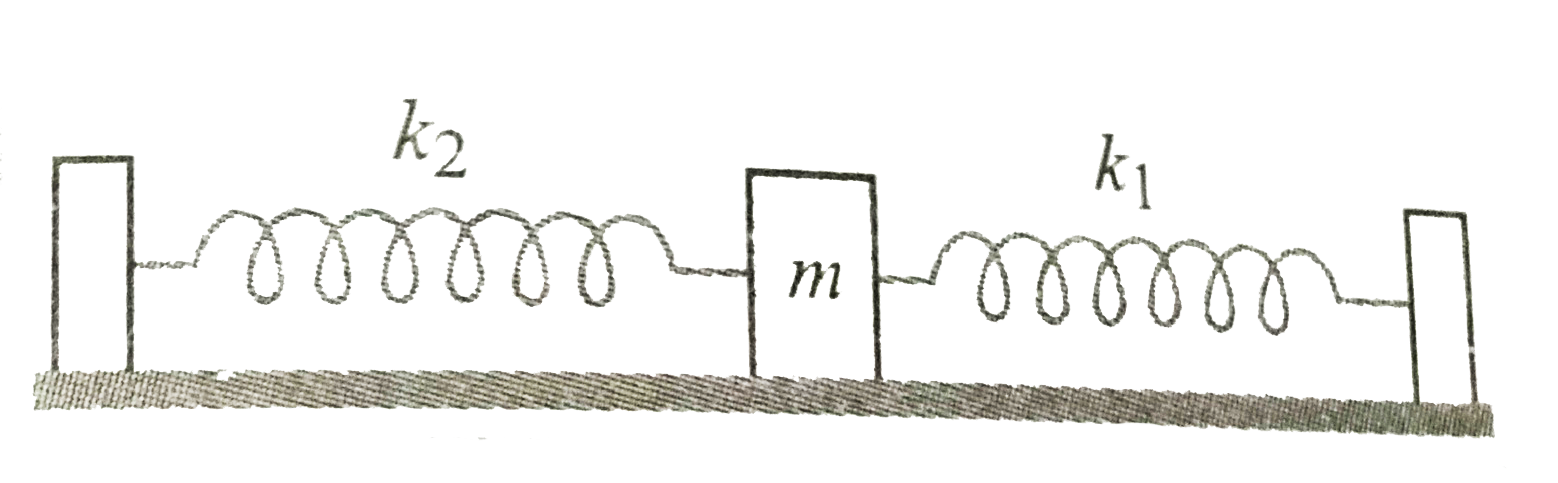
Two springs of force constants k1 and k2 are attached to two opposite sides of a cube of mass m resting on a frictionless table and clamped to two supports at their other ends. Show that if the cube is displaced a little it will execute simple harmonic motion of frequency f=12π√k1+k2m
The correct Answer is:NA
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - NN GHOSHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Eexercies
39 Videos
- SIMPLE AND COMPOUND PENDULUMBOOK - NN GHOSHCHAPTER - SIMPLE AND COMPOUND PENDULUMEXERCISE - Exercise
24 Videos
- SPECIFIC HEAT CAPACITY OF GASESBOOK - NN GHOSHCHAPTER - SPECIFIC HEAT CAPACITY OF GASESEXERCISE - All Questions
17 Videos
Similar Questions
Two springs of force constants k1 and k2 are joined together and the combination is attached to a mass m resting on a frictionless table at one end and clamped to a fixed support at the other. Show the frequency of oscillation of the mass is f=12π√k1k2(k1+k−(2))m
[Hint: Let the mass be displaced by x and the clamped end of the second spring by x′. Then mf = −k1(x−x′). Considering the first spring and the mass as a single system we have mf =−k2x′]
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillation.

View Solution
Knowledge Check
Two spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
 A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)
A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)Two springs have their force constant as k1 and k2(k1>k2). When they are streched by the same force.
ANo work is done in case of both the springsBNo work is done in case of both the springsCNo work is done in case of both the springsDMore work is done in case of first springTwo springs have their force constants K1 and K2 and they are stretched to the same extension. If K2>K1 work done is
Asame in both the springsBmore in springs K1Cmore in springs K2Dindependent of spring constant K
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shwon in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find th eperiod of oscillation.

View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View SolutionTwo spring have force constants k1 and k2 respectively. They are attached to a mass m and two fixed supports as shwon in figure. If the surface is frictionless, fing the time period of oscillations. What is the spring factore of this combination.
View SolutionTwo springs have their force constant as k1 and k2(k1>k2). When they are stretched by the same force.
View SolutionTwo spring have their force constants K1 and K2(K2>K1). When they are stretched by the same force, work done is
View Solution
