Question

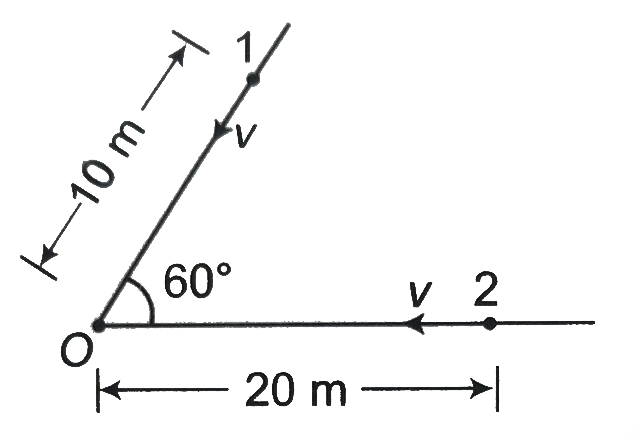
Two straight roads meet an angle of ${60}^{\circ }$. Initially one man is at a distance of $10m$ on one road from the crossing and the other at a distance of $20m$ on the other road from the crossing. They starts moving at the same instant with the same speed towards the crossing. find the minimum distance between them.

Explanation

At `t=0`

At `t=t`

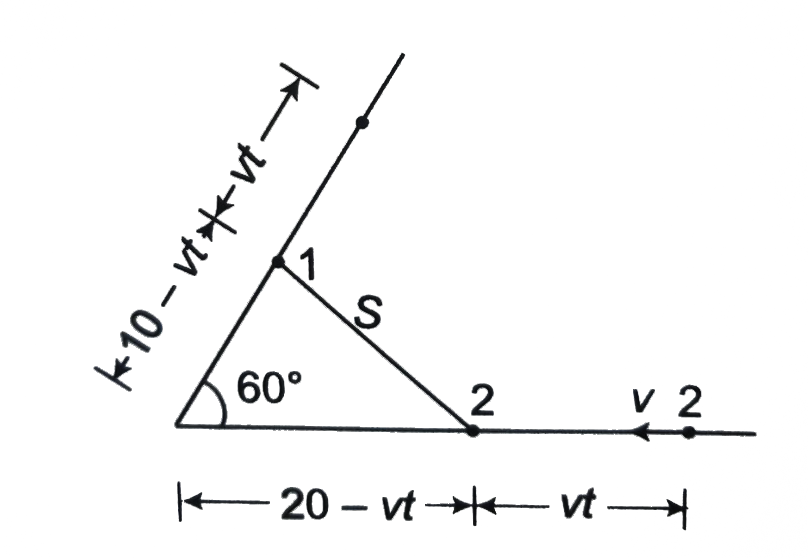
`S^(2)=(10-vt)^(2)+(20-vt)^(2)+2(10-vt)(20-vt)cos 60^(@)`
`=(10-vt)^(2)+(20-vt)^(2)+(200+v^(2)t^(2)-30vt)`
For `S` to be minimum
`(d(S))/(dt)` or `(d(S^(2)))/(dt)=2(10-vt)(-v)+2(20-vt)(-v)+(2v^(2)t-30v)=0`
`vt=15`
`S_(min)=5m`