Two thin rectangular sheets (0.20m×0.40m) are identical. In the first sheet the axis of rotation lies along the 0.20-m side, and in the second it lies along the 0.40-m side. The same torque is applied to each sheet. The first sheet, starting from rest, reaches its final angular velocity in 8.0 s. How long does it take for the second sheet, starting from rest, to reach the same angular velocity?
0.86 s
1.4 s
2.0 s
1.1 s
The correct Answer is:C
To solve the problem, we need to analyze the two sheets and their moments of inertia, as well as the relationship between torque, angular acceleration, and time.
1. Identify the Dimensions and Setup:
- We have two identical rectangular sheets with dimensions 0.20m×0.40m.
- For the first sheet, the axis of rotation is along the 0.20m side.
- For the second sheet, the axis of rotation is along the 0.40m side.
2. Calculate the Moment of Inertia:
- The moment of inertia I for a rectangular sheet about an axis along one of its sides is given by:
I=13mL2
- For the first sheet (axis along 0.20m):
I1=13m(0.40)2=13m(0.16)=0.16m3
- For the second sheet (axis along 0.40m):
I2=13m(0.20)2=13m(0.04)=0.04m3
3. Relate Torque, Angular Acceleration, and Time:
- The torque τ applied to each sheet is related to the moment of inertia and angular acceleration α by:
τ=Iα
- For the first sheet:
τ=I1α1⟹τ=0.16m3α1
- For the second sheet:
τ=I2α2⟹τ=0.04m3α2
4. Set Up the Ratio of Angular Accelerations:
- Since the same torque is applied to both sheets:
0.16m3α1=0.04m3α2
- Canceling m and 13 gives:
0.16α1=0.04α2⟹α2α1=0.160.04=4⟹α2=4α1
5. Relate Time and Angular Velocity:
- The angular velocity ω after time t is given by:
ω=αt
- For the first sheet:
ω=α1t1
- For the second sheet:
ω=α2t2
- Setting the two equations for ω equal gives:
α1t1=α2t2⟹α1t1=4α1t2
- Dividing both sides by α1 (assuming α1≠0):
t1=4t2
6. Substituting Known Values:
- We know t1=8.0s:
8.0=4t2⟹t2=8.04=2.0s
Final Answer:
The time it takes for the second sheet to reach the same angular velocity is 2.0 seconds.
---
- We have two identical rectangular sheets with dimensions 0.20m×0.40m.
- For the first sheet, the axis of rotation is along the 0.20m side.
- For the second sheet, the axis of rotation is along the 0.40m side.
- The moment of inertia I for a rectangular sheet about an axis along one of its sides is given by:
I=13mL2
- For the first sheet (axis along 0.20m):
I1=13m(0.40)2=13m(0.16)=0.16m3
- For the second sheet (axis along 0.40m):
I2=13m(0.20)2=13m(0.04)=0.04m3
- The torque τ applied to each sheet is related to the moment of inertia and angular acceleration α by:
τ=Iα
- For the first sheet:
τ=I1α1⟹τ=0.16m3α1
- For the second sheet:
τ=I2α2⟹τ=0.04m3α2
- Since the same torque is applied to both sheets:
0.16m3α1=0.04m3α2
- Canceling m and 13 gives:
0.16α1=0.04α2⟹α2α1=0.160.04=4⟹α2=4α1
- The angular velocity ω after time t is given by:
ω=αt
- For the first sheet:
ω=α1t1
- For the second sheet:
ω=α2t2
- Setting the two equations for ω equal gives:
α1t1=α2t2⟹α1t1=4α1t2
- Dividing both sides by α1 (assuming α1≠0):
t1=4t2
- We know t1=8.0s:
8.0=4t2⟹t2=8.04=2.0s
The time it takes for the second sheet to reach the same angular velocity is 2.0 seconds.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (More than One Option Correct Type)2videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS(Linked Comprehension)3videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PROBLEMS41videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
Similar Questions
From a rectangular metal sheet of sides 25 cm and 20 cm, a circular sheet as large as possible is cut-off. What is the area of the remaining sheet?
View SolutionThe area of a rectangular sheet is 500m2. If the length of the sheet is 25cm, what is its width? Also find the perimeter of the rectangular sheet.
View Solution
Knowledge Check
- Question 1 - Select One
What is the magnitude of the average acceleration of a skier who, starting from rest, reaches a speed of 8.0 m/s when going down a slope for 5.0 s ?
A0.85m/s2B1.1m/s2C1.6m/s2D1.9m/s2 - Question 2 - Select One
A rock, dropped from rest near the surface of an atmosphere-free planet, attains a speed of 20.0 m/s after falling 8.0 m.
How long would it take the object, falling from rest, to fall 16 m on this planet ?A0.8 sB2.5 sC1.1 sD3.5 s - Question 3 - Select One
Two cars move in the same direction along parallel roads. One of them is a 200m, long travelling with a velocity of 20m/s. The second one is 800m long travelling with a velocity of 7.5m/s. How long will it take for the first car to overtake the second car?
A20sB40sC60sD80s
A wheel rotating at an angular speed of 20 rad/s ils brought to rest by a constant trouque in 4.0 secons. If the moiment of inertia of the wheel about the axis of rotation is 0.20 kg−m2 find the work done by the torque in the first two seconds.
View Solutionfrom a rectangular sheet of tin, of size 100 cm by 80 cm, are cut four squares of side 10 cm from each corner. Find the area of the remaining sheet.
View SolutionTwo heavy metallic plates are joined together at 90∘ to each other. A laminar sheet of mass 30kg is hinged at the line AB joining the two heavy metallic plates. The hinges are frictionless. The moment of inertia of the laminar sheet about an axis parallel to AB and passing through its center of mass is 1.2 kg m2. Two rubber obstacles P and Q are fixed, one on each metallic plate at a distance 0.5m from the line AB. This distance is chosen so that the reaction due to the hinges on the laminar sheet is zero during the impact. Initially the laminar sheet hits one of the obstacles with an angular velocity 1 rad/s and turns back. If the impulse on the sheet due to each obstacle is 6 N-s,
(a) Find the location of the center of mass of the laminar sheet from AB.
(b) At what angular velocity does the laminar sheet come back after the first impact?
(c) After how many impacts, does the laminar sheet come to rest?
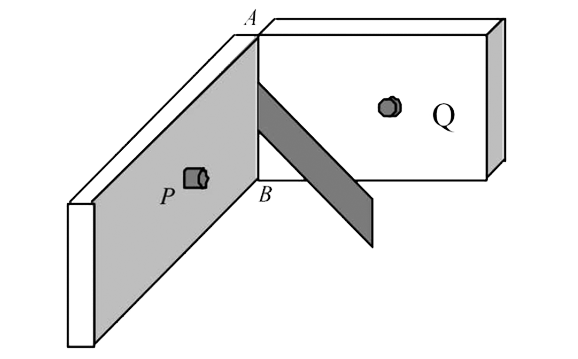 View Solution
View SolutionA motorboat starting from rest on a lake acceleration line at a constant rate of 3.0m/s2 for 8.0s. How far does the boat travel during this time ?
View SolutionA particle starts with an initial velocity 2.0 m/s along the positive x-direction and it accelerations uniformly at the rate of 0.40m/s2
(a) Find the distance travelled by it in the first three seconds.
(b) How much time does it take to reach the velocity 9.0 m/s?
(c) How much distance will it cover in reaching the velocity 9.0 m/s?View Solution

