Two unequal blocks placed over each other of densities σ1 and σ2 are immersed in a fluid of density of σ. The block of density σ1 is fully submerged so that ratio of their masses is 12 and σ/σ1=2 and σ/σ2=0.5. Find the degree of submergence of the upper block of density σ2.
50% submerged
25% submerged
75% submerged
fully submerged
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have two blocks with densities σ1 and σ2 placed over each other. The block with density σ1 is fully submerged in a fluid of density σ. Given the ratios of their masses and the densities, we need to find the degree of submergence of the upper block with density σ2.
Step 2: Given Information
1. The ratio of the masses of the two blocks is m1m2=12.
2. The density ratios are given as:
- σσ1=2 which implies σ1=σ2.
- σσ2=0.5 which implies σ2=2σ.
Step 3: Express Masses in Terms of Volume
Let the volumes of the blocks be V1 for the block with density σ1 and V2 for the block with density σ2.
- The mass of block 1:
m1=σ1V1=(σ2)V1
- The mass of block 2:
m2=σ2V2=(2σ)V2
Step 4: Use the Mass Ratio
From the mass ratio m1m2=12:
σ2V12σV2=12
Cross-multiplying gives:
σV1=2⋅2σV2⟹V1=4V2
Step 5: Buoyant Force and Weight Balance
The block with density σ1 is fully submerged, so the buoyant force acting on it is:
Fb=σV1g
The total weight of both blocks is:
W=m1g+m2g=(σ2V1+2σV2)g
Step 6: Set Up the Equation
Setting the total weight equal to the buoyant force:
σV1=(σ2V1+2σV2)
Dividing through by σ (assuming σ≠0):
V1=12V1+2V2
Rearranging gives:
12V1=2V2⟹V1=4V2
This confirms our earlier finding.
Step 7: Degree of Submergence of Block 2
Let x be the fraction of the volume of block 2 that is submerged. The volume of block 2 is V2, so the volume submerged is xV2.
The buoyant force on block 2 is:
Fb=σ(xV2)g
Setting the total weight equal to the buoyant force:
(2σV2)g=σ(xV2)g
Cancelling g and σ (assuming σ≠0):
2V2=xV2
Dividing both sides by V2 (assuming V2≠0):
2=x
Thus, x=2, which means the upper block is fully submerged.
Conclusion
The degree of submergence of the upper block of density σ2 is 100% or fully submerged.
---
We have two blocks with densities σ1 and σ2 placed over each other. The block with density σ1 is fully submerged in a fluid of density σ. Given the ratios of their masses and the densities, we need to find the degree of submergence of the upper block with density σ2.
1. The ratio of the masses of the two blocks is m1m2=12.
2. The density ratios are given as:
- σσ1=2 which implies σ1=σ2.
- σσ2=0.5 which implies σ2=2σ.
Let the volumes of the blocks be V1 for the block with density σ1 and V2 for the block with density σ2.
m1=σ1V1=(σ2)V1
- The mass of block 2:
m2=σ2V2=(2σ)V2
From the mass ratio m1m2=12:
σ2V12σV2=12
Cross-multiplying gives:
σV1=2⋅2σV2⟹V1=4V2
The block with density σ1 is fully submerged, so the buoyant force acting on it is:
Fb=σV1g
The total weight of both blocks is:
W=m1g+m2g=(σ2V1+2σV2)g
Setting the total weight equal to the buoyant force:
σV1=(σ2V1+2σV2)
Dividing through by σ (assuming σ≠0):
V1=12V1+2V2
Rearranging gives:
12V1=2V2⟹V1=4V2
This confirms our earlier finding.
Let x be the fraction of the volume of block 2 that is submerged. The volume of block 2 is V2, so the volume submerged is xV2.
Fb=σ(xV2)g
Setting the total weight equal to the buoyant force:
(2σV2)g=σ(xV2)g
Cancelling g and σ (assuming σ≠0):
2V2=xV2
Dividing both sides by V2 (assuming V2≠0):
2=x
Thus, x=2, which means the upper block is fully submerged.
The degree of submergence of the upper block of density σ2 is 100% or fully submerged.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
Two paralle plane sheets 1 and 2 carry uniform charge densites σ1andσ2 (see fig. The electric field in the region marked I is (σ1>σ2):

View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If σ is the surface tension the diameter of the drop of the liquid is
View SolutionThe sum of series Σ∞n=12n2n+1! is
View SolutionAn object of w and density ρ is submerged in liquid of density σ, its apparent weight will be
View SolutionTwo spherical conductors of radii 4cmand5cm are charged to the same potential. If σ1andσ2 be respective value of surface density of charge on both the conductors, then the ratio of σ1/σ2 will be
View SolutionElectrical conductivies of Ge and Na are σ1 and σ2 respectively. If these substances are heard, then
View SolutionTwo thin infinite parallel plates have uniform charge densities +σ and −σ. The electric field in the space between them is
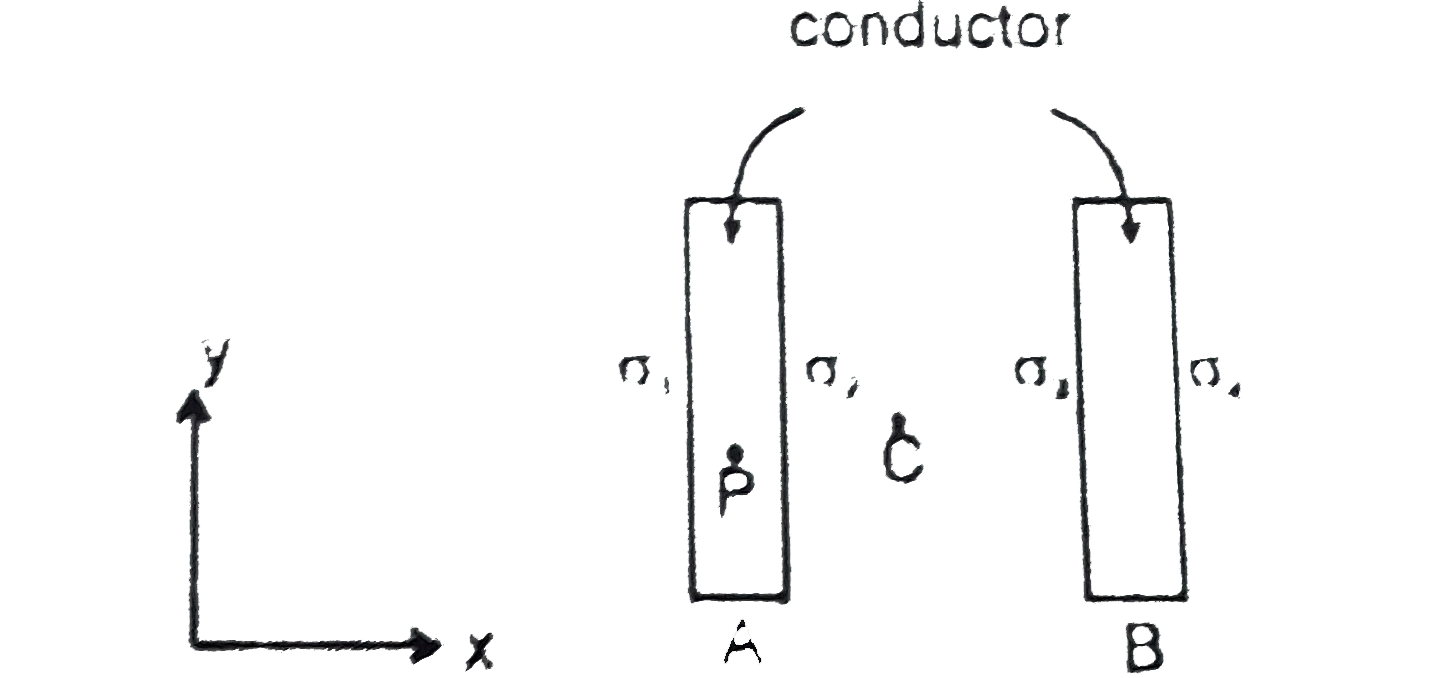
View SolutionFigure shown two infinitely large conducting plates A and B. If electric field at C due to charge densities σ1,σ2,σ3 and σ40 is Eˆi, find σ2 and σ3 in terms of E. Derive a relation between σ1 and σ4.
View SolutionA ball of radius r and density ρ is moving in a liquid of density σ1 and then in a liquid of density simga3. The velocity of the ball remains same in all the three liquids. (Givenσ3>σ2>σ1). If n1,n2andn3 are their coefficients of viscosity , then which of the following is always true ?

View SolutionThe energy of σ2s, is greater than that of σ∗1s orbital because
View Solution