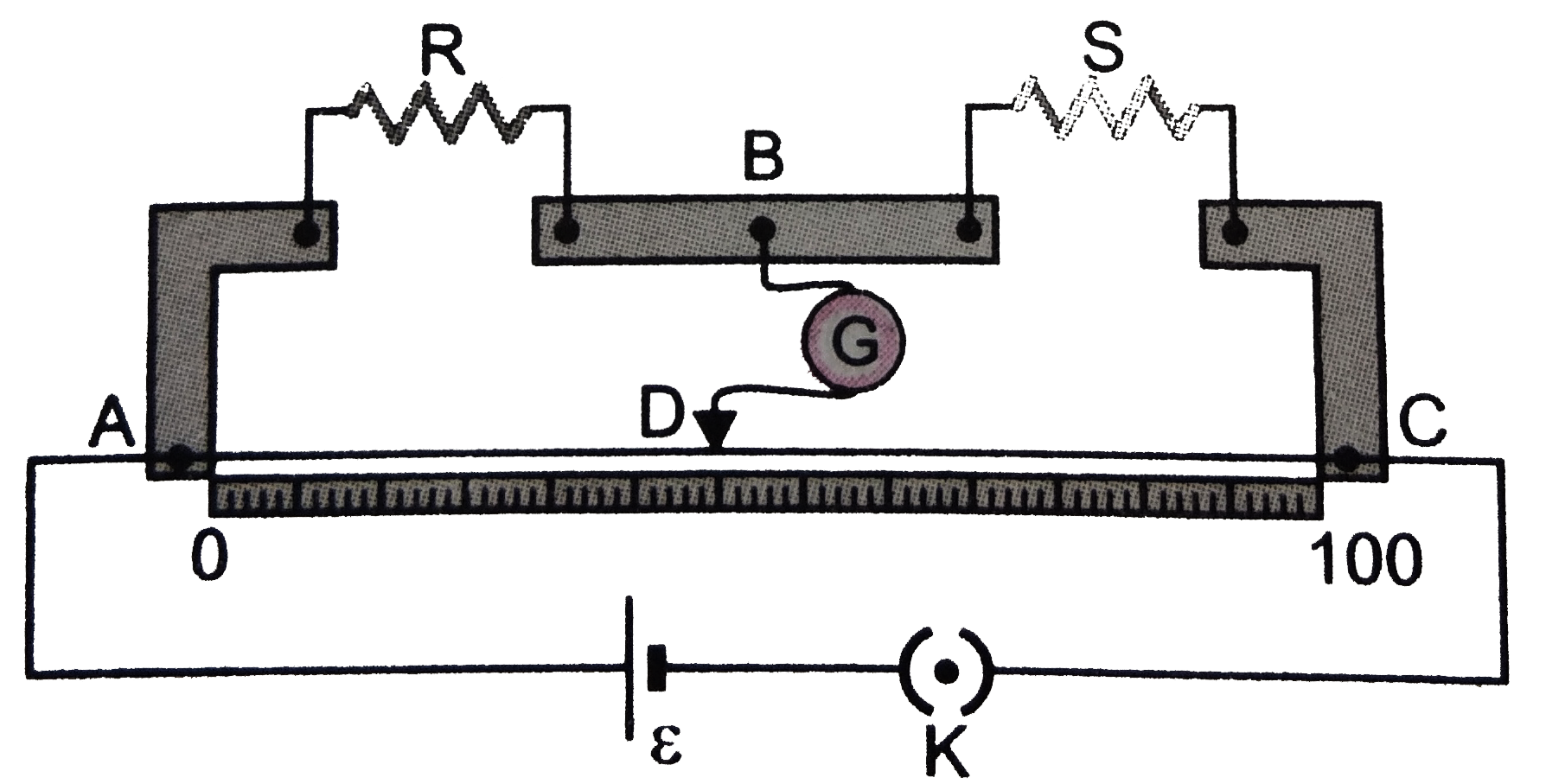
Two unknown resistances X and Y are placed on the left and right gaps of a meter bridge. The null point in the galvanometer is obtained at a distance of 80cm from left. A resistance of 100Ω is now connected in parallel across X. The null point is then found by shifting the sliding contact toward left by 20cm. Calculate X and Y.
To solve the problem of finding the unknown resistances X and Y using a meter bridge, we can follow these steps:
Step 1: Understand the initial conditions
In the first case, the null point is obtained at a distance of 80cm from the left. This means that the length of the wire on the left side (where resistance X is connected) is 80cm and the length on the right side (where resistance Y is connected) is 20cm (since the total length of the meter bridge is 100cm).
Step 2: Apply the balance condition
According to the principle of the meter bridge (based on Wheatstone's bridge), the balance condition can be expressed as:
XY=Length on leftLength on right=8020
This simplifies to:
XY=4(Equation 1)
From this, we can express X in terms of Y:
X=4Y
Step 3: Analyze the second condition
In the second case, a 100Ω resistor is connected in parallel with X. The effective resistance X′ of the left gap now becomes:
X′=100X100+X
The null point shifts left by 20cm, meaning the new length on the left side is 60cm and the length on the right side is 40cm.
Step 4: Apply the balance condition again
Using the new lengths, we can write the balance condition again:
X′Y=6040=32(Equation 2)
Substituting X′=100X100+X into the equation gives:
100X100+XY=32
Cross-multiplying yields:
200X=3Y(100+X)
Expanding this gives:
200X=300Y+3XY
Step 5: Substitute X from Equation 1
Now substitute X=4Y into the equation:
200(4Y)=300Y+3(4Y)Y
This simplifies to:
800Y=300Y+12Y2
Rearranging gives:
12Y2−500Y=0
Factoring out Y:
Y(12Y−500)=0
Thus, Y=0 or Y=50012=1253Ω.
Step 6: Calculate X
Now substitute Y back into X=4Y:
X=4×1253=5003Ω
Final Results
Thus, the values of the resistances are:
X=5003ΩandY=1253Ω
In the first case, the null point is obtained at a distance of 80cm from the left. This means that the length of the wire on the left side (where resistance X is connected) is 80cm and the length on the right side (where resistance Y is connected) is 20cm (since the total length of the meter bridge is 100cm).
According to the principle of the meter bridge (based on Wheatstone's bridge), the balance condition can be expressed as:
XY=Length on leftLength on right=8020
This simplifies to:
XY=4(Equation 1)
From this, we can express X in terms of Y:
X=4Y
In the second case, a 100Ω resistor is connected in parallel with X. The effective resistance X′ of the left gap now becomes:
X′=100X100+X
The null point shifts left by 20cm, meaning the new length on the left side is 60cm and the length on the right side is 40cm.
Using the new lengths, we can write the balance condition again:
X′Y=6040=32(Equation 2)
Substituting X′=100X100+X into the equation gives:
100X100+XY=32
Cross-multiplying yields:
200X=3Y(100+X)
Expanding this gives:
200X=300Y+3XY
Now substitute X=4Y into the equation:
200(4Y)=300Y+3(4Y)Y
This simplifies to:
800Y=300Y+12Y2
Rearranging gives:
12Y2−500Y=0
Factoring out Y:
Y(12Y−500)=0
Thus, Y=0 or Y=50012=1253Ω.
Now substitute Y back into X=4Y:
X=4×1253=5003Ω
Thus, the values of the resistances are:
X=5003ΩandY=1253Ω
Topper's Solved these Questions
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Subjective
18 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Single Correct
94 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - Solved Examples
4 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.5
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - compression type
7 Videos
Similar Questions
In a meter bridge, the null point is found at a distance of 40cm from A. If a resistance of 12Ω in connected in parallel with S the null point occurs at 50.0cm from A Determine the value of R and S

View SolutionCircuit diagram of metre bridge is shown in figure. The null point is found at a distance of 40cm from A. it now a resistance of 12Ω is connected in parallel with S, the null point occurs at 64cm.

View SolutionIn a metre bridge the null point is found at a distance of 35 cm from A. If now a resistance of 10Ω is connected in parallel with S, the null point occurs at 50 cm. Determine the values of R and S.
View SolutionTwo unkonwn resistances X and Y are connected to left and right gaps of a meter bridge and the balancing point is obtained at 80cm from left. When a 10Ω resistance is connected parallel to X, the balancing point is 50cm from left. The values of X and Y respectively are
View SolutionIn a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 Ω is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.

View SolutionIn a meter bridge,
the null points is found at a distance of 33.7 cm from A. If now a resistance of 12Ω is connected in parallel with S, the null point occurs at 51.9 cm. Determine the values of R and S.
View SolutionWhen un known resistance and a resistance of 4Ω are used in the left and right gaps of a meter bridge, the balance point is 50cm. the shift in the balance point if a 4Ω resistance is now connected parallel to the resistor in right gap ______
View SolutionIn a meter bridge, the null point is found at a distance of l1cm from A. if now a resistance of X is connected in parallel with S, the null point occurs at l2cm. Obtain a formula for X is terms of l1,l2andS.
View SolutionThe resistance in the left and right gaps of a balanced meter bridge are R1 and R1. The balanced point is 50cm. If a resistance of 24Ω is connected in parallel to R2, the balance point is 70cm. The value of R1 or R2 is.
View SolutionTwo unknown resistances are connected in two gaps of a meter-bridge. The null point is obtained at 40 cm from left end. A 30Ω resistance is connected in series with the smaller of the two resistances, the null point shifts by 20 cm to the right end. The value of smaller resistance in Ω is
View Solution
