The resistance in the left and right gaps of a balanced meter bridge are R1 and R1. The balanced point is 50cm. If a resistance of 24Ω is connected in parallel to R2, the balance point is 70cm. The value of R1 or R2 is.
12Ω
8 Omega
16Ω
32Ω
The correct Answer is:D
To solve the problem, we will use the principles of a meter bridge and the concept of resistances in parallel.
1. Understanding the Initial Setup:
In a balanced meter bridge, the ratio of the resistances is equal to the ratio of the lengths from the ends of the bridge to the balance point. Given that the balance point is at 50 cm, we can set up our first equation:
R1R2=50100−50=5050=1
This implies:
R1=R2
2. Introducing the Parallel Resistance:
When a resistance of 24 Ω is connected in parallel to R2, the equivalent resistance Req of R2 and the 24 Ω resistor can be calculated using the formula for resistors in parallel:
Req=R2⋅24R2+24
3. Setting Up the New Balance Point:
With the new balance point at 70 cm, we can set up the second equation:
R1Req=70100−70=7030=73
4. Substituting R1 with R2:
Since we established that R1=R2, we can substitute R1 in the second equation:
R2R2⋅24R2+24=73
5. Cross-Multiplying to Solve for R2:
Cross-multiplying gives us:
R2⋅(R2+24)=73⋅24
Simplifying the right side:
R2⋅(R2+24)=56
6. Expanding and Rearranging:
Expanding the left side:
R22+24R2−56=0
7. Using the Quadratic Formula:
We can solve this quadratic equation using the quadratic formula:
R2=−b±√b2−4ac2a
Here, a=1,b=24,c=−56:
R2=−24±√242−4⋅1⋅(−56)2⋅1
R2=−24±√576+2242
R2=−24±√8002
R2=−24±20√22
R2=−12±10√2
8. Calculating the Positive Root:
Since resistance cannot be negative, we take the positive root:
R2=−12+10√2
9. Finding R1:
Since R1=R2, we conclude:
R1=R2=−12+10√2≈32Ω
Final Answer:
Both R1 and R2 are approximately 32 Ω.
In a balanced meter bridge, the ratio of the resistances is equal to the ratio of the lengths from the ends of the bridge to the balance point. Given that the balance point is at 50 cm, we can set up our first equation:
R1R2=50100−50=5050=1
This implies:
R1=R2
When a resistance of 24 Ω is connected in parallel to R2, the equivalent resistance Req of R2 and the 24 Ω resistor can be calculated using the formula for resistors in parallel:
Req=R2⋅24R2+24
With the new balance point at 70 cm, we can set up the second equation:
R1Req=70100−70=7030=73
Since we established that R1=R2, we can substitute R1 in the second equation:
R2R2⋅24R2+24=73
Cross-multiplying gives us:
R2⋅(R2+24)=73⋅24
Simplifying the right side:
R2⋅(R2+24)=56
Expanding the left side:
R22+24R2−56=0
We can solve this quadratic equation using the quadratic formula:
R2=−b±√b2−4ac2a
Here, a=1,b=24,c=−56:
R2=−24±√242−4⋅1⋅(−56)2⋅1
R2=−24±√576+2242
R2=−24±√8002
R2=−24±20√22
R2=−12±10√2
Since resistance cannot be negative, we take the positive root:
R2=−12+10√2
Since R1=R2, we conclude:
R1=R2=−12+10√2≈32Ω
Both R1 and R2 are approximately 32 Ω.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.83videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery49videos
FLUID MECHANICS
Similar Questions
Two unkonwn resistances X and Y are connected to left and right gaps of a meter bridge and the balancing point is obtained at 80cm from left. When a 10Ω resistance is connected parallel to X, the balancing point is 50cm from left. The values of X and Y respectively are
View SolutionIn a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 Ω is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
A3B6C9D12
Two resistances are connected in two gaps of a meter bridge. The balance point is 20cm from the zero end. A resistance of 15Ω is connected in series with the smaller of the two. The null point shifts to 40cm. The value of the smaller resistance in Ω is
View SolutionIn a metre bridge the null point is found at a distance of 35 cm from A. If now a resistance of 10Ω is connected in parallel with S, the null point occurs at 50 cm. Determine the values of R and S.
View SolutionIn a meter bridge, the null point is found at a distance of 40cm from A. If a resistance of 12Ω in connected in parallel with S the null point occurs at 50.0cm from A Determine the value of R and S
 View Solution
View SolutionIn a meter bridge,
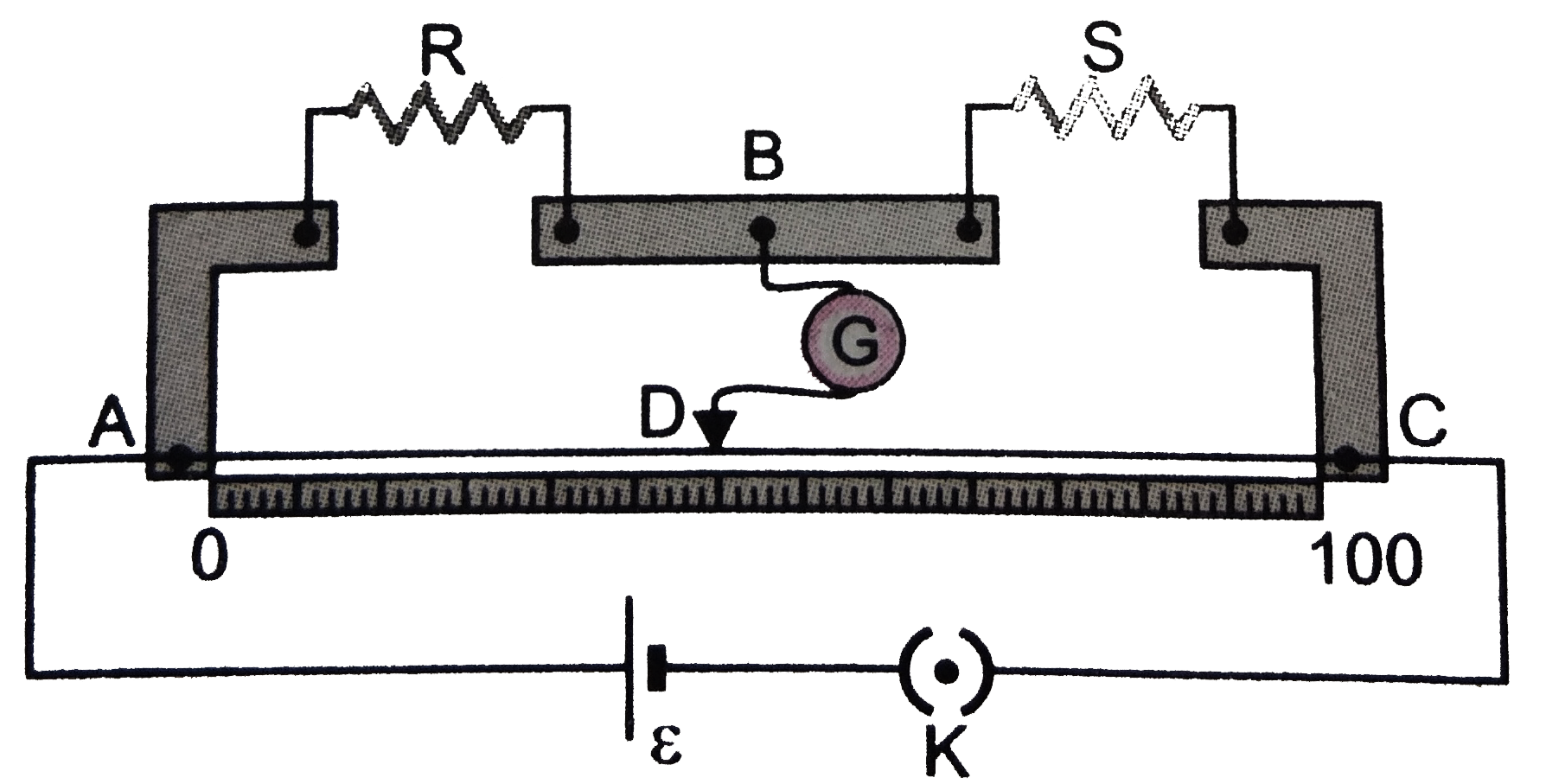
the null points is found at a distance of 33.7 cm from A. If now a resistance of 12Ω is connected in parallel with S, the null point occurs at 51.9 cm. Determine the values of R and S.View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View SolutionAn unknown resistance R1 is connected is series with a resistance of 10Ω. This combination is connected to one gap of a meter bridge, while other gap is connected to another resistance R2. The balance point is at 50cm Now , when the 10Ω resistance is removed, the balanced point shifts to 40cm Then the value of R1 is.
View Solution

