Two unlike charges of magnitude q are separated by a distance 2d. The potential at a point midway between them is
Zero
14πε0
14πε0.qd
14πε0.2qd2
The correct Answer is:A
To find the electric potential at a point midway between two unlike charges of magnitude q separated by a distance 2d, we can follow these steps:
Step 1: Identify the Charges and Their Positions
Let’s denote the two charges as +q and −q. Place the positive charge +q at position A and the negative charge −q at position B. The distance between the two charges is 2d.
- Position of +q (Charge 1): A (let's say at x=−d)
- Position of −q (Charge 2): B (let's say at x=+d)
Step 2: Determine the Midpoint
The midpoint P between the two charges is located at x=0. The distance from the midpoint to each charge is d.
Step 3: Calculate the Potential Due to Each Charge
The electric potential V due to a point charge is given by the formula:
V=k⋅qr
where k is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where the potential is being calculated.
- Potential at point P due to charge +q:
V1=k⋅(+q)d
- Potential at point P due to charge −q:
V2=k⋅(−q)d
Step 4: Calculate the Total Potential at the Midpoint
The total electric potential V at point P is the algebraic sum of the potentials due to both charges:
V=V1+V2
Substituting the values we calculated:
V=k⋅(+q)d+k⋅(−q)d
V=kqd−kqd
V=0
Conclusion
The electric potential at the midpoint between the two unlike charges is 0.
---
Let’s denote the two charges as +q and −q. Place the positive charge +q at position A and the negative charge −q at position B. The distance between the two charges is 2d.
- Position of −q (Charge 2): B (let's say at x=+d)
The midpoint P between the two charges is located at x=0. The distance from the midpoint to each charge is d.
The electric potential V due to a point charge is given by the formula:
V=k⋅qr
where k is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where the potential is being calculated.
V1=k⋅(+q)d
V2=k⋅(−q)d
The total electric potential V at point P is the algebraic sum of the potentials due to both charges:
V=V1+V2
Substituting the values we calculated:
V=k⋅(+q)d+k⋅(−q)d
V=kqd−kqd
V=0
The electric potential at the midpoint between the two unlike charges is 0.
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Relation Between Electric Field And Potential
24 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Electric Potential Energy
22 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Knowledge Check
Two point charges Q and −Q/4 are separated by a distance X. Then
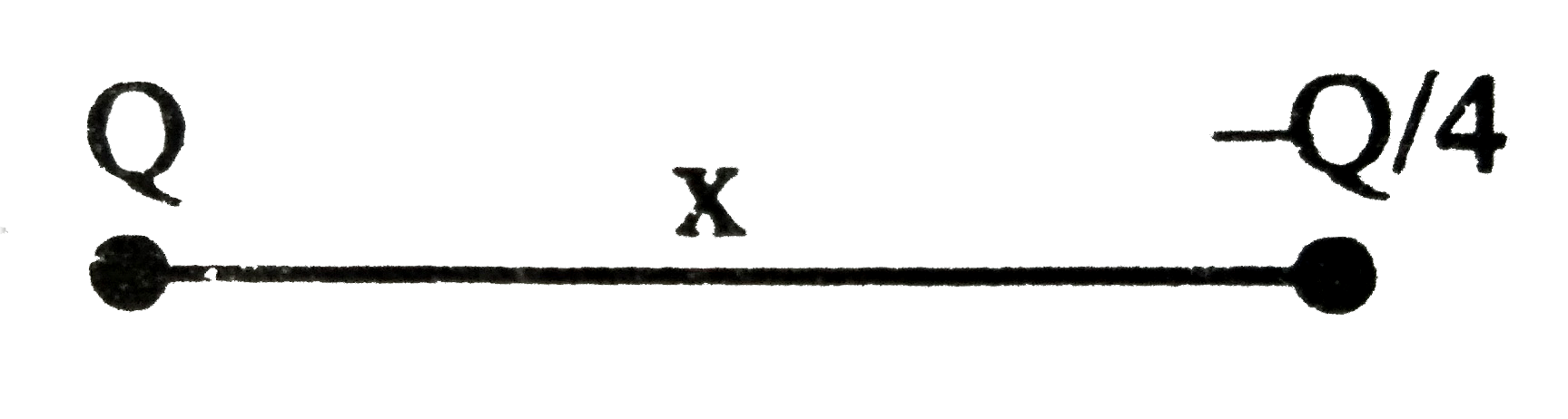 .Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.
.Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.Two cahrges of 50μC and 100μC are separated by a distance of 0.6m .The intensity of electric filed at a point midway between them is
A50×106v/MB5×106M/VC10×106V/mD10XX10−6V/MTwo bodies of masses M1 and M2 are kept separeated by a distance d. The potential at the point where the gravitational field produced by them is zero, is :-
A−Gd(M1+M2+2√M1M2)B−Gd(M1M2+2√M1+M2)C−Gd(M1−M2+2√M1M2)D−Gd(M1M2−2√M1+M2)
Two charges of equal magnitude q are placed at a distance 2a Another charge q of mass m, is placed midway between the two charges on X-axis. If this charges is displaced from equilibruim state to a distance x(x<<a), then the particle :-
View Solutiontwo charge +q and −q are situated at a certain distance. At the point exactly midway between them
View SolutionTwo positive point charges of magnitude Q each are separated by a distance "2a". A test charge 'g0' is located in a plane which is normal to the line joining these charges and midway between them. The locus of the points in this plane for which the force on the test charge has a maximum value is
View SolutionTwo point charges q1=+2C and q2=−1C are separated by a distance d. The position on the line joining the two charges where a third charge q=+1C will be in equilibrium is at a distance
View SolutionTwo points charges +4q and +q are separated by distance r, where should a third point charge Q be placed that the whole system remains in equilibrium
View Solution
