Two wires A and B have the same length and area of cross-secton. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
1
2
1/2
√2
The correct Answer is:B
To solve the problem, we need to find the ratio of the force constants of two wires A and B, given that they have the same length and area of cross-section, but the Young's modulus of wire A is twice that of wire B.
1. Understand the Definitions:
- Young's modulus (Y) is a measure of the stiffness of a material. It is defined as the ratio of stress (force per unit area) to strain (relative change in length).
- The force constant (k) of a wire can be expressed in terms of Young's modulus (Y), the area of cross-section (A), and the original length (L) of the wire.
2. Formula for Force Constant:
- The force constant (k) can be expressed as:
k=Y⋅AL
- Here, Y is Young's modulus, A is the area of cross-section, and L is the original length of the wire.
3. Set Up the Ratio:
- For wire A, the force constant kA is:
kA=YA⋅AL
- For wire B, the force constant kB is:
kB=YB⋅AL
- Now, we can find the ratio of the force constants:
kAkB=YA⋅A/LYB⋅A/L
4. Simplify the Ratio:
- Since the area A and length L are the same for both wires, they cancel out:
kAkB=YAYB
5. Substitute the Given Values:
- We are given that YA=2YB. Therefore, substituting this into the ratio gives:
kAkB=2YBYB=2
6. Final Ratio:
- Thus, the ratio of the force constant of wire A to that of wire B is:
kAkB=2:1
Conclusion:
The ratio of the force constant of wire A to that of wire B is 2:1.
- Young's modulus (Y) is a measure of the stiffness of a material. It is defined as the ratio of stress (force per unit area) to strain (relative change in length).
- The force constant (k) of a wire can be expressed in terms of Young's modulus (Y), the area of cross-section (A), and the original length (L) of the wire.
- The force constant (k) can be expressed as:
k=Y⋅AL
- Here, Y is Young's modulus, A is the area of cross-section, and L is the original length of the wire.
- For wire A, the force constant kA is:
kA=YA⋅AL
- For wire B, the force constant kB is:
kB=YB⋅AL
- Now, we can find the ratio of the force constants:
kAkB=YA⋅A/LYB⋅A/L
- Since the area A and length L are the same for both wires, they cancel out:
kAkB=YAYB
- We are given that YA=2YB. Therefore, substituting this into the ratio gives:
kAkB=2YBYB=2
- Thus, the ratio of the force constant of wire A to that of wire B is:
kAkB=2:1
The ratio of the force constant of wire A to that of wire B is 2:1.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
Knowledge Check
For a given material, Young's modulus is 2.4 times that of rigidity modulus. Its Poisson's ratio is
A2.4B1.2C0.4D0.2A wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAlA wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2L
If Young modulus is three times of modulus of rigidity, then Poisson ratio is equal to
View SolutionTwo wires A and B have the same cross section and are made of the same material, but the length of wire A is twice that of B. Then, for a given load
View SolutionTwo wires A and B of same dimensions are stretched by same amount of force .Young's modulus of A is twice that of B. Which wire will get more elongation?
View SolutionA uniform rod of length 2L, area of cross - section A and Young's modulus Y is lying at rest under the action of three forces as shown.
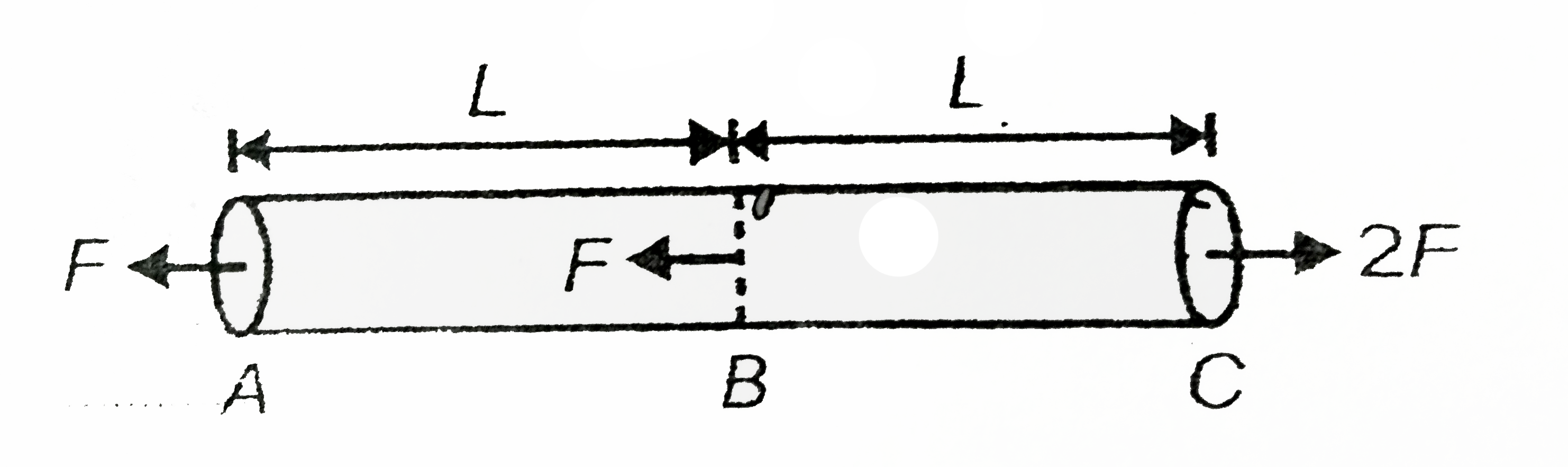
Select the correct alternatives.
View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View Solution
