Two wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
They will be subjected to stresses which are in ratio 2:5
Their lengths will increase in the ratio 5:2
When stretched and released, they will oscillate with time periods in the ratio 5:2
Their time periods will be in the ratio √5:√2
To solve the problem, we need to analyze the relationship between the Young's modulus of the two wires and their time periods when suspended by the same mass M.
1. Understanding Young's Modulus:
Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain=FAΔLL=F⋅LA⋅ΔL
where:
- F = Force applied (equal to the weight of the mass M, i.e., F=Mg)
- A = Cross-sectional area of the wire
- ΔL = Change in length (elongation)
- L = Original length of the wire
2. Relating Young's Modulus to Force Constant:
We can express the force constant K in terms of Young's modulus:
K=A⋅YL
This means that the force constant K is directly proportional to Young's modulus Y.
3. Finding the Ratio of Young's Modulus:
Given that the Young's moduli of the two wires are in the ratio:
Y1Y2=25
We can denote:
- Y1=2k
- Y2=5k
for some constant k.
4. Finding the Ratio of Force Constants:
Since K is directly proportional to Y:
K1K2=Y1Y2=25
5. Finding the Time Period:
The time period T of a mass-spring system (or in this case, a mass suspended by a wire) is given by:
T=2π√MK
Thus, the ratio of the time periods T1 and T2 for the two wires is:
T1T2=√K2K1=√52
6. Final Ratio of Time Periods:
Therefore, the time periods of the two wires are in the ratio:
T1:T2=√5:√2
Conclusion:
The time periods of the two wires when suspended by the same mass M are in the ratio √5:√2.
Young's modulus Y is defined as the ratio of stress to strain:
Y=StressStrain=FAΔLL=F⋅LA⋅ΔL
where:
- F = Force applied (equal to the weight of the mass M, i.e., F=Mg)
- A = Cross-sectional area of the wire
- ΔL = Change in length (elongation)
- L = Original length of the wire
We can express the force constant K in terms of Young's modulus:
K=A⋅YL
This means that the force constant K is directly proportional to Young's modulus Y.
Given that the Young's moduli of the two wires are in the ratio:
Y1Y2=25
We can denote:
- Y1=2k
- Y2=5k
for some constant k.
Since K is directly proportional to Y:
K1K2=Y1Y2=25
The time period T of a mass-spring system (or in this case, a mass suspended by a wire) is given by:
T=2π√MK
Thus, the ratio of the time periods T1 and T2 for the two wires is:
T1T2=√K2K1=√52
Therefore, the time periods of the two wires are in the ratio:
T1:T2=√5:√2
The time periods of the two wires when suspended by the same mass M are in the ratio √5:√2.
Topper's Solved these Questions
Similar Questions
Two wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be

View SolutionTwo wires of equal length and cross sectional area suspended as shown in
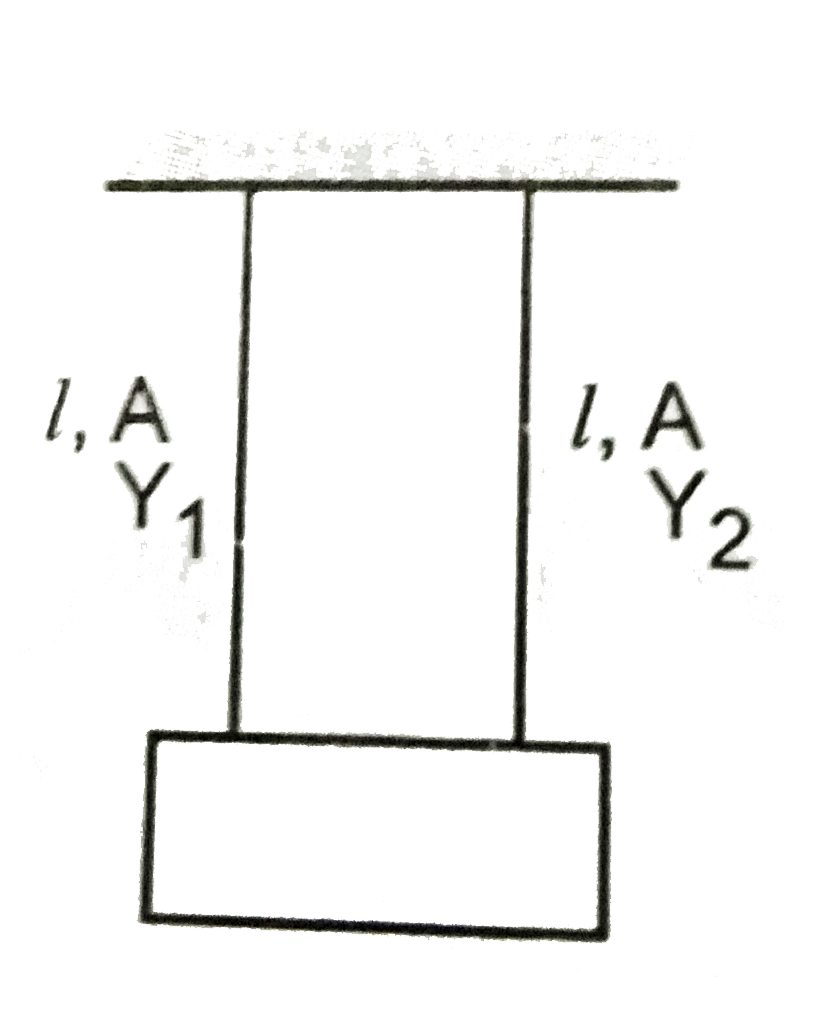
Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View Solution
Knowledge Check
A wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAl
Two wires of equal length and cross sectional area suspended as shown in

Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
View SolutionTwo wires of the same materical having equal area of cross-section have L and 2L. Their respective resistances are in the ratio
View SolutionTwo wires A and B have the same length and area of cross-secton. But Young's modulus of A is two times the Young's modulus of B. Then the ratio of force constant of A to that of B is
View SolutionA wire of natural length l, young's modulus Y and area of cross-section A is extended by x. Then, the energy stored in the wire is given by
View SolutionCalculate the force required to incrase the length of wire of cross-sectional area 10−6m2 by 50% if the Young's modulus of the material of the wire is 90×109Pa.
View SolutionA uniform wire of length 6m and a cross-sectional area 1.2 cm2 is stretched by a force of 600N . If the Young's modulus of the material of the wire 20×1010Nm−2 , calculate (i) stress (ii) strain and (iii) increase in length of the wire.
View SolutionA wire havinga length L and cross- sectional area A is suspended at one of its ends from a ceiling . Density and young's modulus of material of the wire are ρ and Y, respectively. Its strain energy due to its own weight is ρ2g2AL3αY. Find the vqalue of α
View Solution
