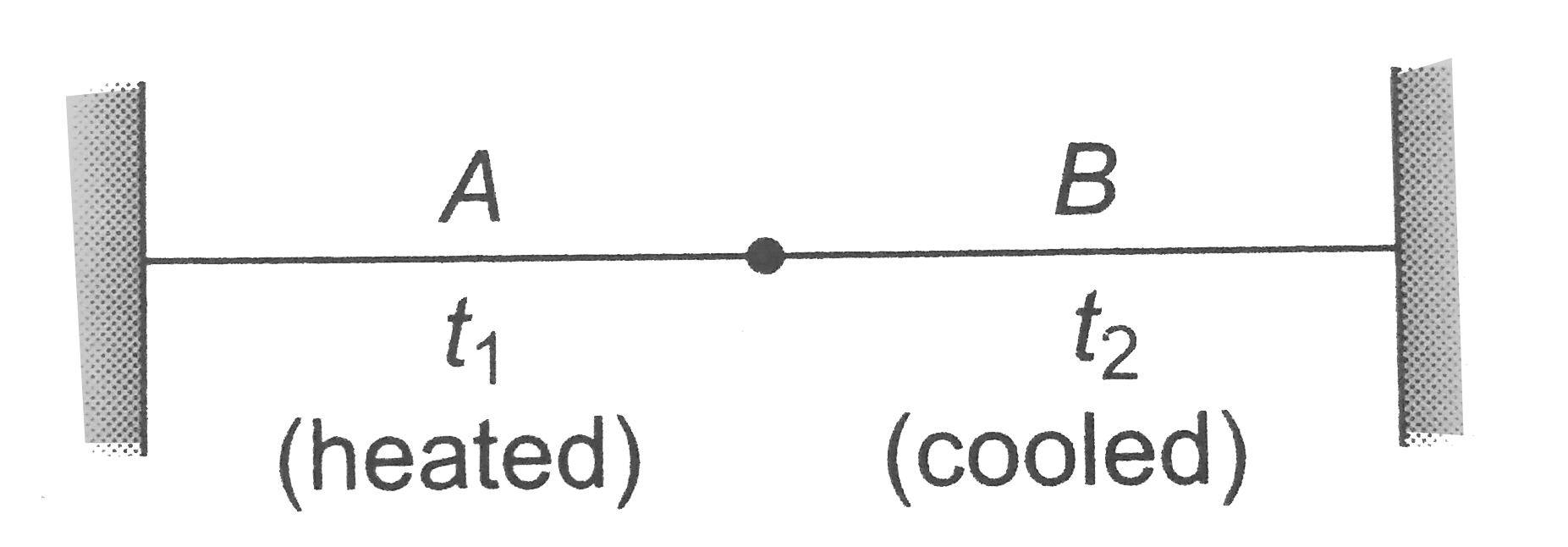
Two wires and of the same cross sectional areas. Young's moduli and and coefficients of linear expansion and respectively are joined together and fixed between rigid supports at either ends. The tension in the compound wire when wire is heated and wire is cooled at different temperature is same when wire alone is cooled at the same temperature as wire earlier.
Find correct oprtion.
The correct Answer is:B
Tension in any wire,
Given
or
For
or, .
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Assertion Reasoning
Explore 21 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:NEET Questions
Explore 47 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Transmission Of Heat : Radiation
Explore 28 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Chapter Test
Explore 29 Videos
- UNIT, DIMENSION AND ERROR ANALYSISBook:A2ZChapter:UNIT, DIMENSION AND ERROR ANALYSISExercise:Chapter Test
Explore 28 Videos
Similar Questions
Two metal rods of the same length and area of cross-section are fixed end to end between rigid supports. The materials of the rods have Young moduli Y1 and Y2 , and coefficient of linear expansion α1 and α2 . The junction between the rod does not shift and the rods are cooled
View SolutionTwo different wires having lengths L1 and L2 and respective temperature coefficient of linear expansion α1 and α2 are joined end - to - end . Then the effective temperature coefficient of linear expansion is :
View Solution
Knowledge Check
Two wire A and B of the same corss sectional area, young's modulli Y1,Y2 and coefficients of linear expansion α1,α2 respectively are joined together and fixed between rigid supports at either ends. The tension in the compound wire when the wire A is heated and Wire B is cooled at different temperature is same when wire A alone in cooled at same temperature as wire B earller. the correct option is
Aα1α2>Y22Y1Bα1α2<Y22Y1Cα1α2>2Y2Y1Dα1α2>Y2Y1Two metal rods of the same length and area of cross-section are fixed end to end between rigid supports. The materials of the rods have Young module Y1 and Y2 , and coefficient of linear expansion α1 and α2 . The junction between the rod does not shift and the rods are cooled
AY1α1=Y2α1BY1α2=Y2α1CY1α21=Y2α22DY21α1=Y22α2Two wires A and B have the same cross section and are made of the same material, but the length of wire A is twice that of B. Then, for a given load
Athe extension of A will be twice that of BBthe extensions of A and B will be equalCthe strain in A will be half that in BDthe strains in A and B will be equal
A metal wire of length jl and area of cross - section A is fixed between rigid supports negligible tension . If this is cooled. The tension in the wire will be
View SolutionTwo wires A and B have the same cross section and are made of the same material, but the length of wire A is twice that of B. Then, for a given load
View SolutionIn a stretched wire under tension and fixed at both ends, the area of cross section of the wire is halved and the tension is doubled. The frequency of the wire will be
View SolutionThe radii and Young's moduli of two uniform wires A and B are in the ratio 2:1 and 1:2 respectively. Both wires are subjected to the same longitudinal force. If the increase in leangth of the wire A is one percent, the percentage increae in length of the wire B is
View SolutionThe radii and Young's moduli of two uniform wires A and B are in the ratio 2:1 and 1:2 respectively. Both wires are subjected to the same longitudinal force. If the increase in length of the wire A is one percent, the percentage increase in length of the wire B is
View Solution
