Two metal rods of the same length and area of cross-section are fixed end to end between rigid supports. The materials of the rods have Young moduli Y1 and Y2 , and coefficient of linear expansion α1 and α2 . The junction between the rod does not shift and the rods are cooled
Y1α1=Y2α2
Y1α2=Y2α1
Y1α21=Y2α22
Y21α1=Y22α2
The correct Answer is:A
To solve the problem, we need to analyze the situation with the two metal rods that are fixed end to end. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Setup
We have two rods of the same length (L) and cross-sectional area (A) made of different materials. The Young moduli of the materials are Y1 and Y2, and their coefficients of linear expansion are α1 and α2. The rods are cooled, which causes them to contract.
Step 2: Condition at the Junction
Since the junction between the rods does not shift, the tension (or stress) in both rods must be the same. This means that the force exerted by both rods is equal.
Step 3: Relate Stress and Strain
Using the definition of Young's modulus:
Y=StressStrain
We can express the stress in terms of tension (T) and area (A):
Y=TA⋅Strain
The strain can be expressed as:
Strain=ΔLL
where ΔL is the change in length due to temperature change.
Step 4: Change in Length Due to Temperature
The change in length for each rod due to temperature change Δθ can be expressed as:
ΔL=α⋅L⋅Δθ
Thus, the strain for each rod becomes:
Strain1=α1LΔθL=α1Δθ
Strain2=α2LΔθL=α2Δθ
Step 5: Equate Tensions
From the definition of Young's modulus, we can express the tensions in both rods:
T1=Y1A⋅Strain1=Y1A⋅α1Δθ
T2=Y2A⋅Strain2=Y2A⋅α2Δθ
Step 6: Set Tensions Equal
Since T1=T2:
Y1Aα1Δθ=Y2Aα2Δθ
We can cancel A and Δθ (assuming Δθ≠0):
Y1α1=Y2α2
Conclusion
Thus, the relationship between the Young moduli and coefficients of linear expansion for the two rods is:
Y1α1=Y2α2
We have two rods of the same length (L) and cross-sectional area (A) made of different materials. The Young moduli of the materials are Y1 and Y2, and their coefficients of linear expansion are α1 and α2. The rods are cooled, which causes them to contract.
Since the junction between the rods does not shift, the tension (or stress) in both rods must be the same. This means that the force exerted by both rods is equal.
Using the definition of Young's modulus:
Y=StressStrain
We can express the stress in terms of tension (T) and area (A):
Y=TA⋅Strain
The strain can be expressed as:
Strain=ΔLL
where ΔL is the change in length due to temperature change.
The change in length for each rod due to temperature change Δθ can be expressed as:
ΔL=α⋅L⋅Δθ
Thus, the strain for each rod becomes:
Strain1=α1LΔθL=α1Δθ
Strain2=α2LΔθL=α2Δθ
From the definition of Young's modulus, we can express the tensions in both rods:
T1=Y1A⋅Strain1=Y1A⋅α1Δθ
T2=Y2A⋅Strain2=Y2A⋅α2Δθ
Since T1=T2:
Y1Aα1Δθ=Y2Aα2Δθ
We can cancel A and Δθ (assuming Δθ≠0):
Y1α1=Y2α2
Thus, the relationship between the Young moduli and coefficients of linear expansion for the two rods is:
Y1α1=Y2α2
Similar Questions
A metal rod of length l, cross-sectional area A, Young's modulus Y and coefficient of linear expansion α is heated to t∘C. The work that can be performed by the rod when heated is
View SolutionTwo rods of length l1 and l2 are made of material whose coefficient of linear expansion are α1 and α2 , respectively. The difference between their lengths will be independent of temperatiure if l1/l2 is to
View SolutionThere are two rods of length l1 and l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.
View SolutionTwo different wires having lengths L1 and L2 and respective temperature coefficient of linear expansion α1 and α2 are joined end - to - end . Then the effective temperature coefficient of linear expansion is :
View SolutionTwo rods having length l1 and l2, made of materials with the linear coefficient of expansion α1 and α2 were welded together. The equivalent coefficients of linear expansion for the obtained rod:-

View SolutionTwo metallic rods of length l and 3l have coefficient of linear expansion α and 3α respectively. The coefficient of linear expansion ofr their series combinations, is
View SolutionTwo rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l1, coefficient of linear expansion α1 and Young's modulus Y1. The correcsponding quantities for second rod are l2,α2 and Y2. The temperature of both the rods is now raised by t∘C.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.

View SolutionTwo rods of different metals having the same area of cross section A are placed between the two massive walls as shown is Fig. The first rod has a length l1, coefficient of linear expansion α1 and Young's modulus Y1. The correcsponding quantities for second rod are l2,α2 and Y2. The temperature of both the rods is now raised by t∘C.
i. Find the force with which the rods act on each other (at higher temperature) in terms of given quantities.
ii. Also find the length of the rods at higher temperature.

View SolutionA thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
View SolutionFour rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
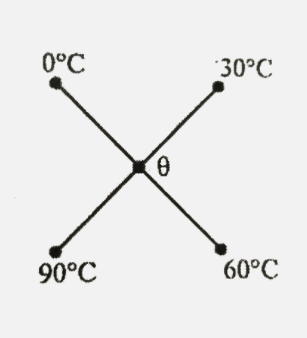
View Solution
