Two wires are held perpendicular to the plane of paper and are 5 m apart. They carry currents of 2.5 A and 5 A in same direction. Then, the magnetic field strength (B) at a point midway between the wires will be
μ04πT
μ02πT
3μ02πT
3μ04πT
The correct Answer is:b
To find the magnetic field strength (B) at a point midway between two wires carrying currents in the same direction, we can follow these steps:
Step 1: Identify the setup
We have two parallel wires that are 5 m apart. The first wire carries a current of I1=2.5A and the second wire carries a current of I2=5A. The point of interest is located midway between the two wires, which means it is 2.5 m from each wire.
Step 2: Use the formula for the magnetic field due to a long straight current-carrying wire
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space (μ0≈4π×10−7T m/A).
Step 3: Calculate the magnetic field due to the first wire
For the first wire (2.5 A):
- Distance from the point to the wire, r=2.5m
B1=μ0⋅2.52π⋅2.5=μ04π
Step 4: Calculate the magnetic field due to the second wire
For the second wire (5 A):
- Distance from the point to the wire, r=2.5m
B2=μ0⋅52π⋅2.5=μ0π
Step 5: Determine the direction of the magnetic fields
Using the right-hand rule:
- For the first wire (2.5 A), the magnetic field at the midpoint will be directed into the plane of the paper (let's denote this as negative).
- For the second wire (5 A), the magnetic field at the midpoint will be directed out of the plane of the paper (let's denote this as positive).
Step 6: Calculate the net magnetic field
Since the magnetic fields are in opposite directions, we can find the net magnetic field by subtracting the smaller from the larger:
Bnet=B2−B1=μ0π−μ04π=4μ04π−μ04π=3μ04π
Step 7: Substitute μ0 to find the numerical value
Substituting μ0=4π×10−7T m/A:
Bnet=3(4π×10−7)4π=3×10−7T=3×10−7T
Final Answer
The magnetic field strength at the point midway between the wires is:
Bnet=3×10−7T
---
We have two parallel wires that are 5 m apart. The first wire carries a current of I1=2.5A and the second wire carries a current of I2=5A. The point of interest is located midway between the two wires, which means it is 2.5 m from each wire.
The magnetic field B at a distance r from a long straight wire carrying current I is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space (μ0≈4π×10−7T m/A).
For the first wire (2.5 A):
- Distance from the point to the wire, r=2.5m
B1=μ0⋅2.52π⋅2.5=μ04π
For the second wire (5 A):
- Distance from the point to the wire, r=2.5m
B2=μ0⋅52π⋅2.5=μ0π
Using the right-hand rule:
- For the first wire (2.5 A), the magnetic field at the midpoint will be directed into the plane of the paper (let's denote this as negative).
- For the second wire (5 A), the magnetic field at the midpoint will be directed out of the plane of the paper (let's denote this as positive).
Since the magnetic fields are in opposite directions, we can find the net magnetic field by subtracting the smaller from the larger:
Bnet=B2−B1=μ0π−μ04π=4μ04π−μ04π=3μ04π
Substituting μ0=4π×10−7T m/A:
Bnet=3(4π×10−7)4π=3×10−7T=3×10−7T
The magnetic field strength at the point midway between the wires is:
Bnet=3×10−7T
Topper's Solved these Questions
Similar Questions
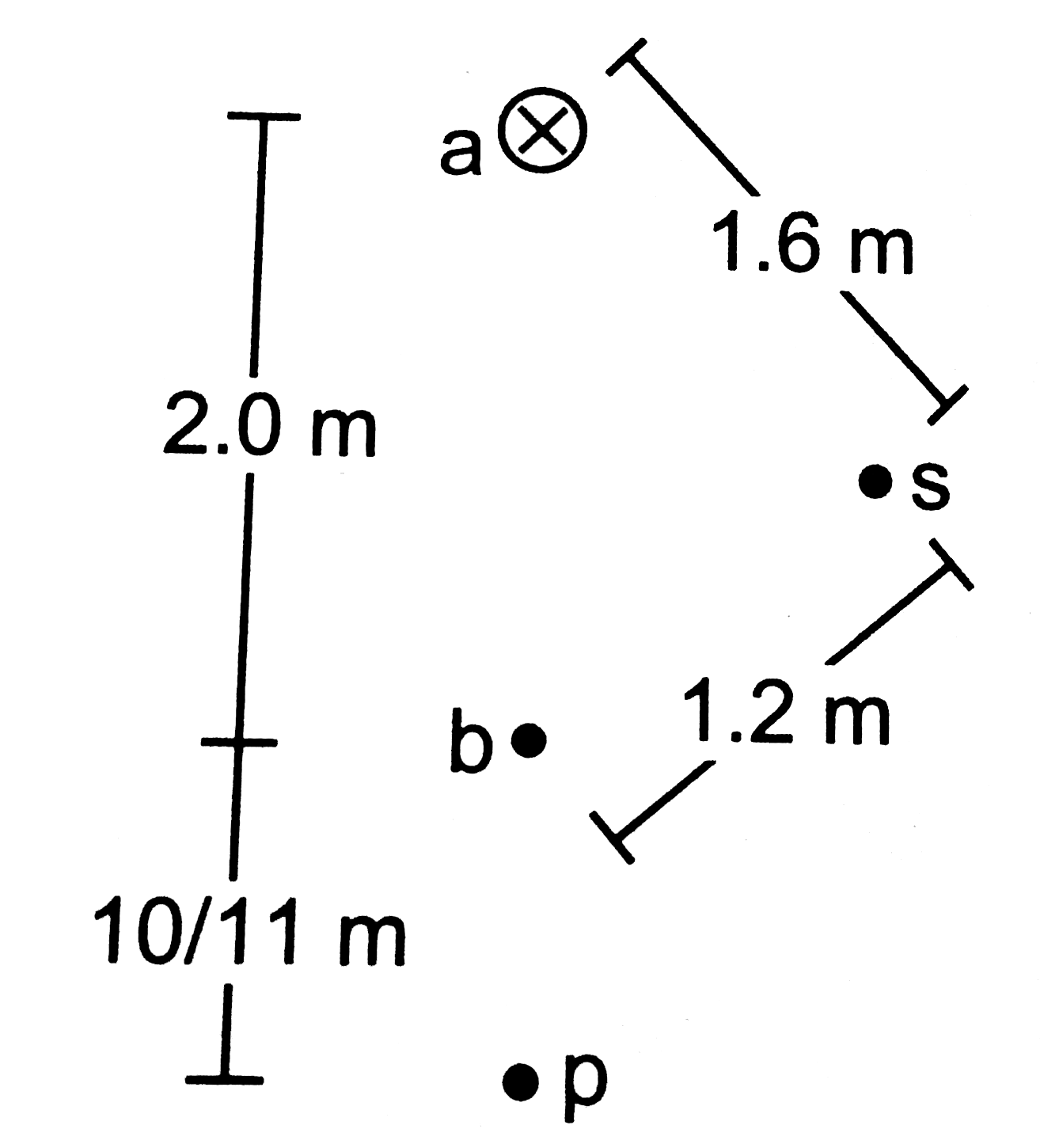
Two long, straight wires a and b are 2⋅0 m apart,
perpendicular to the plane of the paper as shown in figure
. The wire a carries a current of 9⋅6A directed
into the plane of the figure,The magnetic field at the
point P at a distance of 10/11 m from the wire b is zero.
Find (a) the magnitude and direction of the current in b,
(b) the magnitude of the magnetic field B at the point s
and (c) the force per unit length on the wire b.
View SolutionTwo infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
View Solution
Knowledge Check
Two long parallel wires P and Q are both perpendicular to the plane of the paper with distance 5m between them. If P and Q carry current of 2.5 amp and 5 amp respectively in the same direction, then the magnetic field at a point half way between the wires is
A√3μ02πBμ0πC3μ02πDμ02πTwo parallel wires 2 m apart carry currents of 2 A and 5 A respectively in same direction, the force per unit length acting between these two wires is
A2×10−6Nm−1B3×10−6Nm−1C1×10−6Nm−1D4×10−6Nm−1Two infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
ATwice the magnetic field produced due to each of the wiresBHalf of the magnetic field produced due to each of the wiresCSquare of the magnetic field produced due to each of the wiresDZero
Two long straight wires are arranged parallel to each other and are kept 10 cm apart in vacuum. They carry currents of 5A and 10A respectively in the same direction. What is the magnetic force on a lergth of 20 cm of either wire ?
View SolutionTwo parallel wires carry currents of 20A and 40A in same direction. Another wire carrying a current anti- parallel to 20A is placed midway between the two wires. The magnetic force on it will be
View SolutionTwo long parallel wires are 30 cm apart carrying currents 10 A and 15 A respectively in the same direction. The force acting over a length of 5 m of the wires is
View SolutionTwo parallel conductors A and B separated by 5cm carry electric current of 6A and 2A in the same direction. The point between A and B where the field is zero at
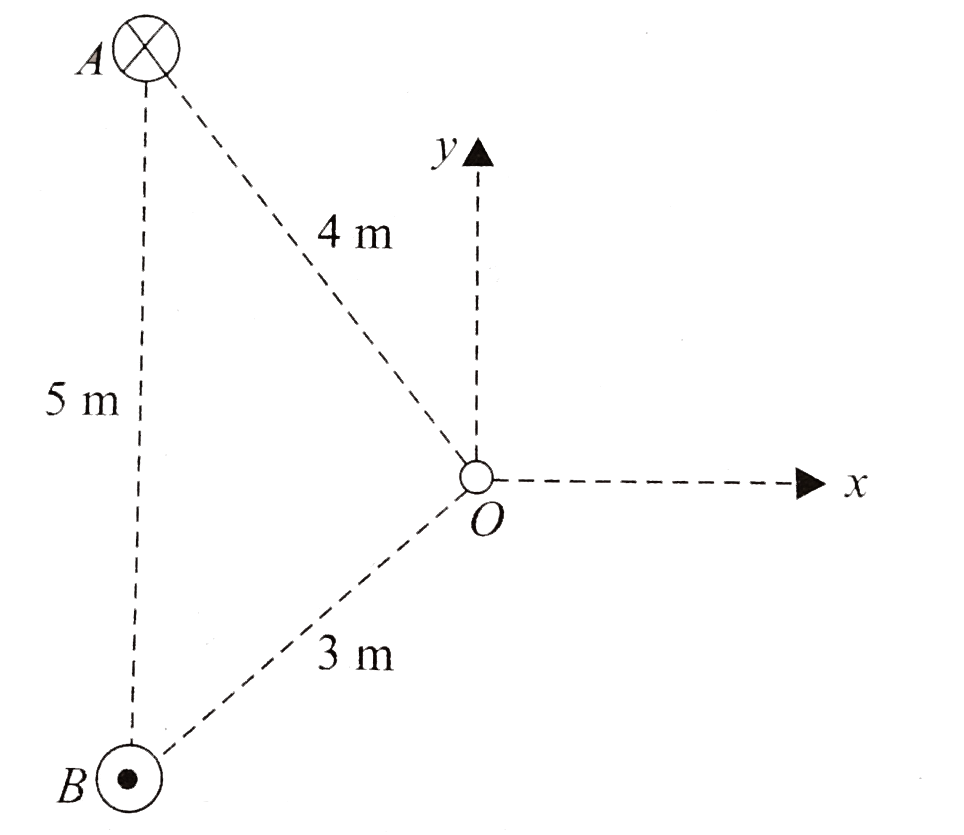
View SolutionTwo infinitely long straight parallel wire are 5 m apart, perpendicular to the plane of paper. One of the wires, as it passes perpendicular to the plane of paper, intersects it at A and carries current I in the downward direction. The other wire intersects the plane of paper at point B and carries current k int the outward direction O in the plane of paper as shown in Fig. With x and y axis shown, magnetic induction at O in the component form can be expressed as
View Solution
