Two wires are stretched under tension of T1andT2 such that T2>T1, producing 4 beats per seconds on vibrating. When the tension in one of them is changed slightly even then the beat frequency remains 4. Which of the two T1orT2 should be increased or decreased ?
To solve the problem, we need to analyze the relationship between tension in the wires and their frequencies, and how changes in tension affect the beat frequency.
1. Understanding the Frequencies:
The frequency of a wire under tension is given by the formula:
f=12L√Tμ
where T is the tension, L is the length of the wire, and μ is the mass per unit length.
2. Identifying the Relationship:
From the formula, we can see that frequency f is directly proportional to the square root of the tension T:
f∝√T
Therefore, if T2>T1, it follows that f2>f1.
3. Given Information:
The problem states that the beat frequency is 4 beats per second, which means:
|f2−f1|=4
4. Effect of Changing Tensions:
We need to determine how changing either T1 or T2 affects the beat frequency.
5. Increasing T2:
If we increase T2, then f2 will increase. This will increase the difference |f2−f1|, which will lead to a beat frequency greater than 4. Hence, increasing T2 is not a viable option.
6. Decreasing T2:
If we decrease T2, f2 will decrease, which could potentially reduce the difference |f2−f1|. If T2 is decreased sufficiently, it may reach a point where the beat frequency could drop below 4, which is also not a suitable option.
7. Increasing T1:
If we increase T1, then f1 will increase. This could potentially reduce the difference |f2−f1| and bring it closer to 4 beats per second.
8. Decreasing T1:
If we decrease T1, f1 will decrease, which will increase the difference |f2−f1| and lead to a beat frequency greater than 4.
9. Conclusion:
The only way to maintain a beat frequency of 4 beats per second after changing the tension is to increase T1 or decrease T2. Both options can satisfy the condition of keeping the beat frequency constant.
Final Answer:
To maintain the beat frequency of 4 beats per second, you should increase T1 or decrease T2.
The frequency of a wire under tension is given by the formula:
f=12L√Tμ
where T is the tension, L is the length of the wire, and μ is the mass per unit length.
From the formula, we can see that frequency f is directly proportional to the square root of the tension T:
f∝√T
Therefore, if T2>T1, it follows that f2>f1.
The problem states that the beat frequency is 4 beats per second, which means:
|f2−f1|=4
We need to determine how changing either T1 or T2 affects the beat frequency.
If we increase T2, then f2 will increase. This will increase the difference |f2−f1|, which will lead to a beat frequency greater than 4. Hence, increasing T2 is not a viable option.
If we decrease T2, f2 will decrease, which could potentially reduce the difference |f2−f1|. If T2 is decreased sufficiently, it may reach a point where the beat frequency could drop below 4, which is also not a suitable option.
If we increase T1, then f1 will increase. This could potentially reduce the difference |f2−f1| and bring it closer to 4 beats per second.
If we decrease T1, f1 will decrease, which will increase the difference |f2−f1| and lead to a beat frequency greater than 4.
The only way to maintain a beat frequency of 4 beats per second after changing the tension is to increase T1 or decrease T2. Both options can satisfy the condition of keeping the beat frequency constant.
To maintain the beat frequency of 4 beats per second, you should increase T1 or decrease T2.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - REVISION EXERCISES107videos
WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - MULTIPLE CHOICE QUESTIONS88videos
WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - NCERT EXEMPLAR PROBLEMS31videos
WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - CHAPTER PRACTICE TEST15videos
UNITS AND MEASUREMENT
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Chapter Practice Test16videos
WORK, ENERGY AND POWER
Similar Questions
Knowledge Check
- Question 1 - Select One
When temperature of a reaction mixture is changed from T1 to T2 half life is found to decrease thus,
AT2>T1 and the reaction is endothermicBT2>T1 and the reaction is exothermicCT1>T2 and the reaction is endothermicDT2>T1 and the reaction can be endothermic or exothermic - Question 2 - Select One or More
Two idential straight wires are stretched so as to produce 6 beats per second when vibrating simultaneously. On changing the tension slightly in one of them, the beat frequency remains unchanged. Denoting by T1, T2 the higher and the lower initial tension in the strings, then it could be said that while making the above changes in tension,
A(a) T2 was decreasedB(b) T2 was increasedC( c ) T1 was decreasedD(d) T1 was increased - Question 3 - Select One
Two identical strings are stretched at tensions TA and TB. A truning fork is used to set them in vibration. A vibrates in its fundamental mode and B in its second harmonic mode.
ATA=2TBBTA=4TBC2TA=TBD4TA=TB
Determine the tension T1 and T2 in the strings shown in Fig.
 View Solution
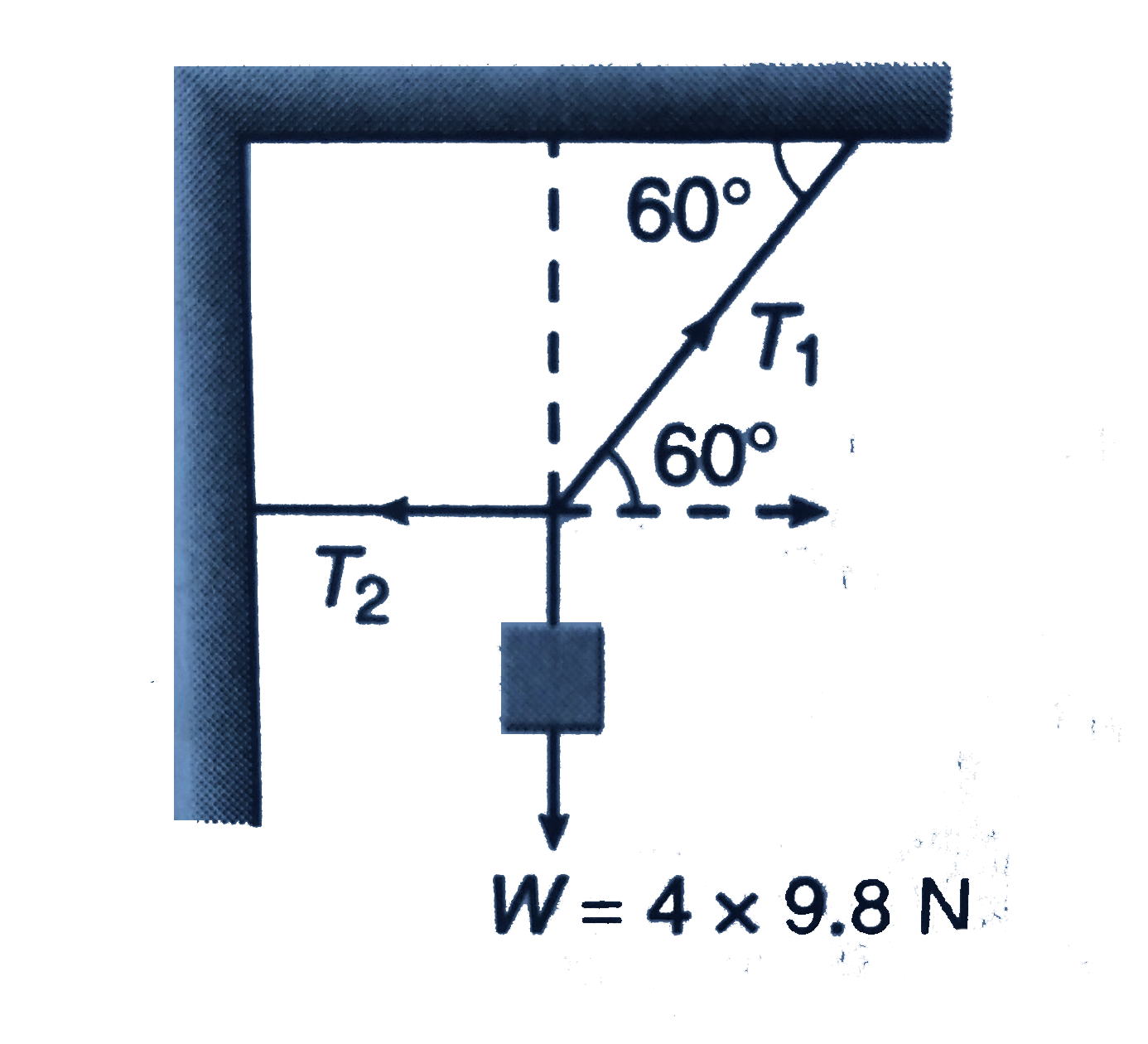
View SolutionDetermine the tensions T1 and T2 in the string as shown in figure.
 View Solution
View SolutionTwo identical wires are put under same tension and have same frequency of vibration. When tension in one of the wire is increased by 2%, then 6 beats/sec can be heard. What will be the original frequency of the wires ?
View SolutionTwo identical straight wires are stretched so as to products 6beats/s when vibrating simultaneously. On changing the tension slightly in one of them, the beat frequency remains unchanged. Denoting by T2 , T2 the higher and the lower initial tension in the strings, then it could be said that that while making the above changes in tension
(a) T2 was decreased
(b) T2 was decreased
(c) T1 was decreased
(d) T1was decreasedView SolutionA piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire B produces 6 beats per second with it when the tension in A is slightly increased. Find the ratio of the tension in A to the tension in B.
View Solution