Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is Pa and that of brass is Pa.
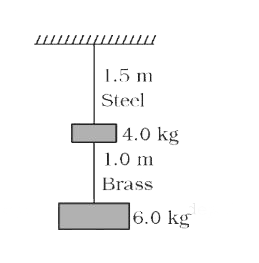
Elongation of the steel wire =
Elongation of the brass wire =
Diameter of the wires, d = 0.25 m
Hence, the radius of the wires, = 0.125 cm
Length of the steel wire, = 1.5 m
Length of the brass wire, = 1.0 m
Total force exerted on the steel wire:
= 98 N
Young's modulus for steel:
Where,
= Change in the length of the steel wire
= Area of cross-section of the steel wire =
Young’s modulus of steel, pa
Total force on the brass wire:
Young’s modulus for brass:
Where,
= Change in length
= Area of cross-section of the bass wire
Elongation of the steel wire = 1.49m
Elongation of the brass wire = 1.3m
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE21videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERTCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE31videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERTCHAPTER - MOTION IN A PLANE EXERCISE - EXERCISE32videos
MOTION IN A PLANE
Similar Questions
Two wires of diameter 0.25cm, one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is 1.5m and that of brass is 1.0m. Young's modulus of steel is 2.0×1011Pa and that of brass is 1.0×1011 Pa. Compute the ratio of elongations of steel and brass wires. △lsteel△lbrass=?
 View Solution
View SolutionYoung 's modulus of steel is 2.0×1011Nm/(2). Express it is dynecm2.
View SolutionCompute the elongation of the steel wire and brass wire in the given
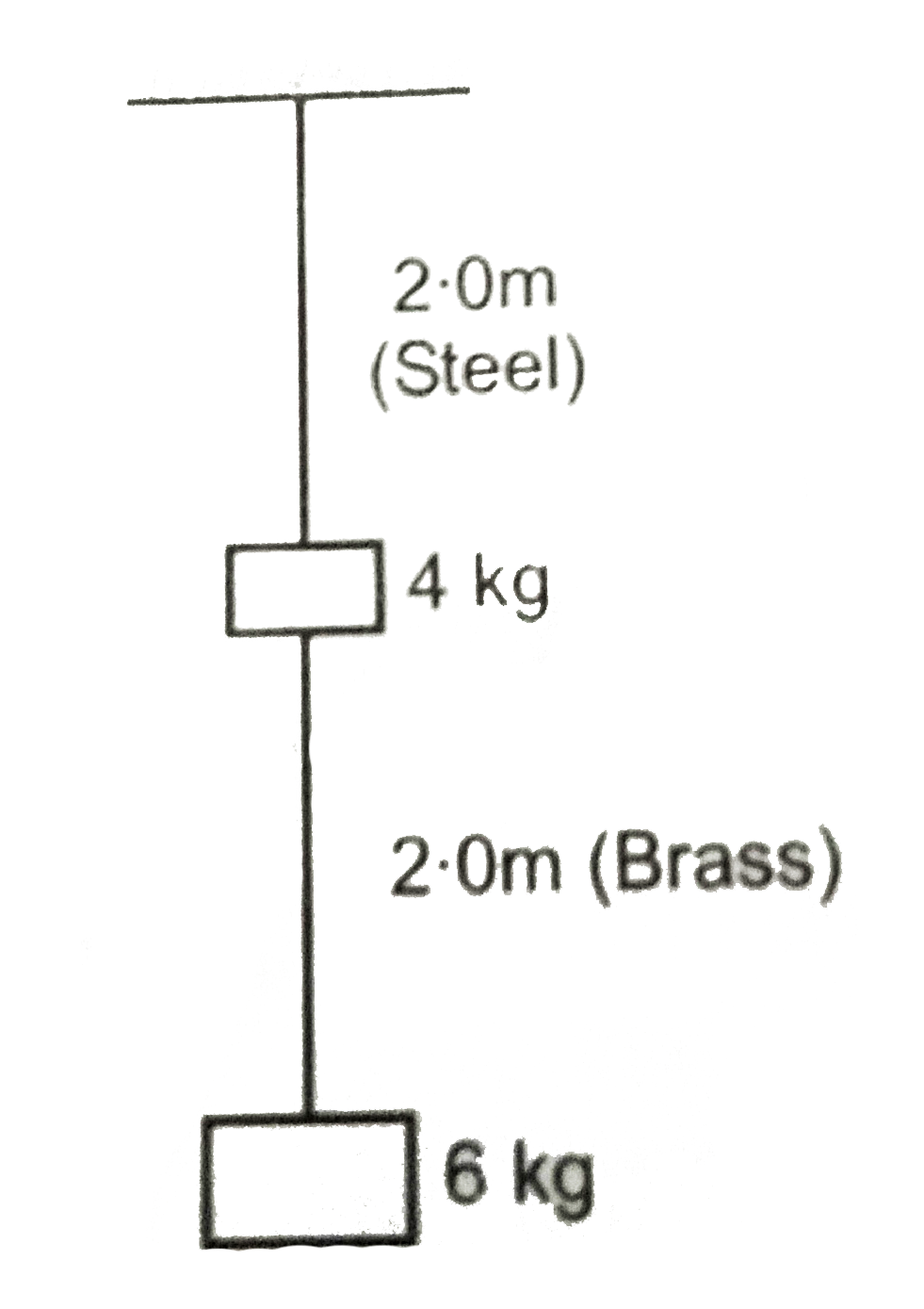
Given unloaded length of steel wire = 2.0 m, unloaded length of brass wire = 1.0m. Area of cross-section of each wire =0.049cm2.
Ysteel=2×1011Pa
and YBrass=0.90×1011Pa,g=9.8ms−2View SolutionCompute the elongation of the steel wire in the figure. Unloaded length of the steel wire =1.5 m, the diameter of the wire is 0.25 m, Young's modulus of steel is 2×1011 N m−2.
View SolutionTwo wires of equal cross section but one made of steel and the other of copper, are joined end to end. When the combination is kept under tension, the elongations in the two wires are found to be equal. Find the ratio of the lengths of the two wires. Young modulus of steel =2.0×1011Nm−2 and that of copper =1.1×101Nm−2
View SolutionA steel wire of length 4 m and diameter 5 mm is stretched by kg-wt. Find the increase in its length if the Young's modulus of steel wire is 2.4×1012dynecm−2
View SolutionThe speed of longitudinal wave is 100 times, then the speed of transverse wave in a brass wire. What is the stress in wire ? TheYoung's modulus of brass Is 1.0×1011N/m2
View SolutionA steel wire of length 4 m and diameter 5 mm is strethed by 5 kg-wt. Find the increase in its length, if the Young's modulus of steel is 2×1012 dyne cm2
View SolutionA steel wire of length 4m and diameter 5mm is stretched by 5 kg-wt. Find the increase in its length , if the Young's modulus of steel wire is 2⋅4×10−12dyne/cm2
View SolutionA composite wire of uniform diameter 3.0 mm consisting of a copper wire of length 2.2m and a steel wire of length 1.6m stretches under a load by 0.7 mm. Calculate the load, given that the Young's modulus for copper is 1.1×1011Pa and for steel is 2.0×1011Pa.
View Solution

