A composite wire of uniform diameter 3.0 mm consisting of a copper wire of length 2.2m and a steel wire of length 1.6m stretches under a load by 0.7 mm. Calculate the load, given that the Young's modulus for copper is 1.1×1011Pa and for steel is 2.0×1011Pa.
To solve the problem, we need to calculate the load applied to a composite wire made of copper and steel, which stretches under the load. We will use the concept of Young's modulus and the relationship between stress, strain, and Young's modulus.
1. Identify Given Data:
- Diameter of the wire, d=3.0mm=3.0×10−3m
- Length of copper wire, Lc=2.2m
- Length of steel wire, Ls=1.6m
- Total stretch of the composite wire, ΔL=0.7mm=0.7×10−3m
- Young's modulus for copper, Yc=1.1×1011Pa
- Young's modulus for steel, Ys=2.0×1011Pa
2. Calculate the Cross-Sectional Area:
The cross-sectional area A of the wire can be calculated using the formula for the area of a circle:
A=πd24
Substituting the diameter:
A=π(3.0×10−3)24=π(9.0×10−6)4≈7.07×10−7m2
3. Calculate the Stress in Each Wire:
The stress σ in each wire is given by:
σ=FA
where F is the load applied.
4. Calculate the Strain in Each Wire:
The strain ϵ is defined as:
ϵ=ΔLL
For copper:
ϵc=ΔLLc=0.7×10−32.2≈3.18×10−4
For steel:
ϵs=ΔLLs=0.7×10−31.6≈4.38×10−4
5. Relate Stress and Strain using Young's Modulus:
Using the relationship Y=σϵ, we can express the load F for each wire:
For copper:
σc=Yc⋅ϵc⟹Fc=σc⋅A=Yc⋅ϵc⋅A
For steel:
σs=Ys⋅ϵs⟹Fs=σs⋅A=Ys⋅ϵs⋅A
6. Calculate the Total Load:
Since the wires are in series, the load F is the same for both:
F=Fc+Fs
Therefore, we can write:
F=Yc⋅ϵc⋅A+Ys⋅ϵs⋅A
F=A(Yc⋅ϵc+Ys⋅ϵs)
7. Substituting Values:
F=7.07×10−7((1.1×1011)⋅(3.18×10−4)+(2.0×1011)⋅(4.38×10−4))
Calculating each term:
F=7.07×10−7(3.498×107+8.76×107)
F=7.07×10−7⋅1.2258×108≈86.6N
Final Answer:
The load applied to the composite wire is approximately 86.6 N.
- Diameter of the wire, d=3.0mm=3.0×10−3m
- Length of copper wire, Lc=2.2m
- Length of steel wire, Ls=1.6m
- Total stretch of the composite wire, ΔL=0.7mm=0.7×10−3m
- Young's modulus for copper, Yc=1.1×1011Pa
- Young's modulus for steel, Ys=2.0×1011Pa
The cross-sectional area A of the wire can be calculated using the formula for the area of a circle:
A=πd24
Substituting the diameter:
A=π(3.0×10−3)24=π(9.0×10−6)4≈7.07×10−7m2
The stress σ in each wire is given by:
σ=FA
where F is the load applied.
The strain ϵ is defined as:
ϵ=ΔLL
For copper:
ϵc=ΔLLc=0.7×10−32.2≈3.18×10−4
For steel:
ϵs=ΔLLs=0.7×10−31.6≈4.38×10−4
Using the relationship Y=σϵ, we can express the load F for each wire:
For copper:
σc=Yc⋅ϵc⟹Fc=σc⋅A=Yc⋅ϵc⋅A
For steel:
σs=Ys⋅ϵs⟹Fs=σs⋅A=Ys⋅ϵs⋅A
Since the wires are in series, the load F is the same for both:
F=Fc+Fs
Therefore, we can write:
F=Yc⋅ϵc⋅A+Ys⋅ϵs⋅A
F=A(Yc⋅ϵc+Ys⋅ϵs)
F=7.07×10−7((1.1×1011)⋅(3.18×10−4)+(2.0×1011)⋅(4.38×10−4))
Calculating each term:
F=7.07×10−7(3.498×107+8.76×107)
F=7.07×10−7⋅1.2258×108≈86.6N
The load applied to the composite wire is approximately 86.6 N.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Conceptual Problems103videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Advanced problems for competitions21videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Long Answer questions33videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
Similar Questions
A Copper wire of length 2.2m and a steel wire of length 1.6m, both of diameter 3.0mm are connected end to end. When stretched by a load, the net elongation is found to be 0.70 mm. Obtain the load applied . Young's modulus of copper is 1.1×1011Nm−2 and Young's modulus of steel is 2.0×1011Nm−2.
View SolutionA steel wire of length 4 m and diameter 5 mm is stretched by kg-wt. Find the increase in its length if the Young's modulus of steel wire is 2.4×1012dynecm−2
View Solution
Knowledge Check
- Question 1 - Select One
A copper wire of length 4.0mm and area of cross-section 1.2cm2 is stretched with a force of 4.8×103N. If Young's modulus for copper is 1.2×1011N/m2, the increases in the length of the wire will be
A1.33mmB1.33cmC2.66mmD2.66cm - Question 2 - Select One
A steel wire of length 5 m and area of cross-section 4mm2 is stretched by 2 mm by the application of a force. If young's modulus of steel is 2×1011N/m2, then the energy stored in the wire is
A0.64 JB0.16 JC0.32 JD1.28 J
Two wires of diameter 0.25cm, one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is 1.5m and that of brass is 1.0m. Young's modulus of steel is 2.0×1011Pa and that of brass is 1.0×1011 Pa. Compute the ratio of elongations of steel and brass wires. △lsteel△lbrass=?
 View Solution
View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is 2.0×1011Pa and that of brass is 9.1×1011 Pa.
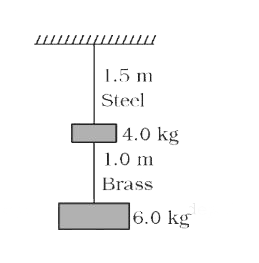 View Solution
View Solution(a) A wire 4m long and 0.3 mm, calculate the potential energy stored in the wire.
Young's modulus for the material of wire is 2.0×1011N/m2.View SolutionA steel wire of length 4 m and diameter 5 mm is strethed by 5 kg-wt. Find the increase in its length, if the Young's modulus of steel is 2×1012 dyne cm2
View SolutionA steel wire of length 4m and diameter 5mm is stretched by 5 kg-wt. Find the increase in its length , if the Young's modulus of steel wire is 2⋅4×10−12dyne/cm2
View SolutionA copper wire 2 m long and 0.5m in diameter supports a mass of 10kg It is stretched by 2.38 mm . Calculate the Young's modulus of the wire.
View Solution

