Under the action of a force →F=(3x)ˆiN , a particle is moving in anticlockwise direction is a square loop of side 3m in x - y plane . What will be the total amount of work done ?
To find the total work done by the force →F=3x^i on a particle moving in an anticlockwise direction along a square loop of side 3 m in the x-y plane, we can follow these steps:
1. Identify the Path of Motion:
The particle moves in an anticlockwise direction around a square loop with vertices at (0,0), (3,0), (3,3), and (0,3).
2. Divide the Path into Segments:
The path can be divided into four segments:
- Segment AB: from (0,0) to (3,0)
- Segment BC: from (3,0) to (3,3)
- Segment CD: from (3,3) to (0,3)
- Segment DA: from (0,3) to (0,0)
3. Calculate Work Done on Each Segment:
- Segment AB (0 to 3 along x-axis):
WAB=∫30→F⋅d→x=∫30(3x^i)⋅(dx^i)=∫303xdx
=3(x22)30=3(92−0)=272 J
- Segment BC (3,0 to 3,3 along y-axis):
Here, the displacement is in the y-direction, and the force has no component in the y-direction.
WBC=0 J
- Segment CD (3,3 to 0,3 along x-axis):
The displacement is in the negative x-direction.
WCD=∫03(3x^i)⋅(dx(−^i))=−∫033xdx=−∫303xdx
=−272 J
- Segment DA (0,3 to 0,0 along y-axis):
Similar to segment BC, the displacement is in the negative y-direction, and again the force has no component in the y-direction.
WDA=0 J
4. Total Work Done:
Now, we sum the work done over all segments:
Wtotal=WAB+WBC+WCD+WDA=272+0−272+0=0 J
Final Answer:
The total amount of work done by the force on the particle as it moves around the square loop is 0 J.
The particle moves in an anticlockwise direction around a square loop with vertices at (0,0), (3,0), (3,3), and (0,3).
The path can be divided into four segments:
- Segment AB: from (0,0) to (3,0)
- Segment BC: from (3,0) to (3,3)
- Segment CD: from (3,3) to (0,3)
- Segment DA: from (0,3) to (0,0)
- Segment AB (0 to 3 along x-axis):
WAB=∫30→F⋅d→x=∫30(3x^i)⋅(dx^i)=∫303xdx
=3(x22)30=3(92−0)=272 J
Here, the displacement is in the y-direction, and the force has no component in the y-direction.
WBC=0 J
The displacement is in the negative x-direction.
WCD=∫03(3x^i)⋅(dx(−^i))=−∫033xdx=−∫303xdx
=−272 J
Similar to segment BC, the displacement is in the negative y-direction, and again the force has no component in the y-direction.
WDA=0 J
Now, we sum the work done over all segments:
Wtotal=WAB+WBC+WCD+WDA=272+0−272+0=0 J
The total amount of work done by the force on the particle as it moves around the square loop is 0 J.
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (A. Multiple Choice Questions)
29 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Objective Type Questions (B. Multiple Choice Questions)
46 Videos
- WORK, ENERGY AND POWER BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Revision Exercise (Long Answer Questions)
9 Videos
- WAVESBOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
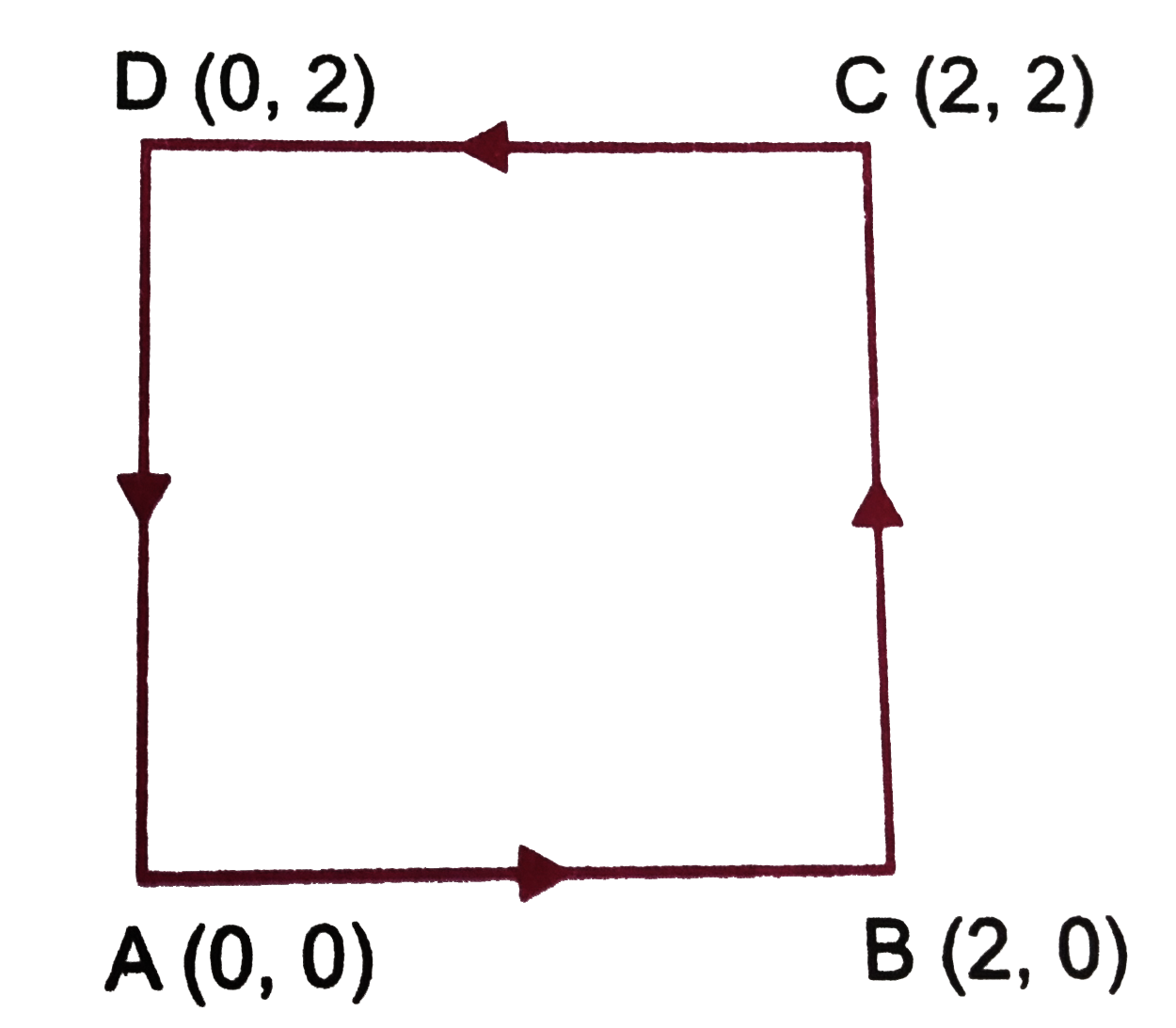
A force →F=2xˆj newton acts in a region where a particle moves annticlockwise in a square loop of 2m in x−y plane as shown in figure . Calculate the total amount of work done. Is this force a conservative force or a non-conservative force?
View SolutionA force →F=(−yˆi+xˆj)N acts on a particle as it moves in an anticlockwise circular motion in x-y plane. The centre of the circle is at the origin. If the work done by the force is 32πJ in one complete revolution then asSigmaing x,y to be in meters, find the radius of the path.
View Solution
Knowledge Check
The work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
A−240JB360JC420JDwill depend upon the pathA particle moves in the x-y plane under the action of a force →F such that the components of its linear momentum →P at any time t are px=costandpy=3sint. What is the magnitude of the vector →F?
A2√2B5C3D4A body of mass 1kg begins to move under the action of a time dependent force →F=(2tˆI+3t2ˆj)N, where ˆi and ˆj are unit vectors along x-and y-axes. What power will be developed by the force at the time t ?
A(2t2+3t3)WB(2t2+4t4)WC(2t3+3t4)WD(2t3+3t5)W
A force F = (4.0xˆi+3.0yˆj) N acts on a particle which moves in the x-direction from the origin to x = 5.0 m. Find the work done on the object by the force.
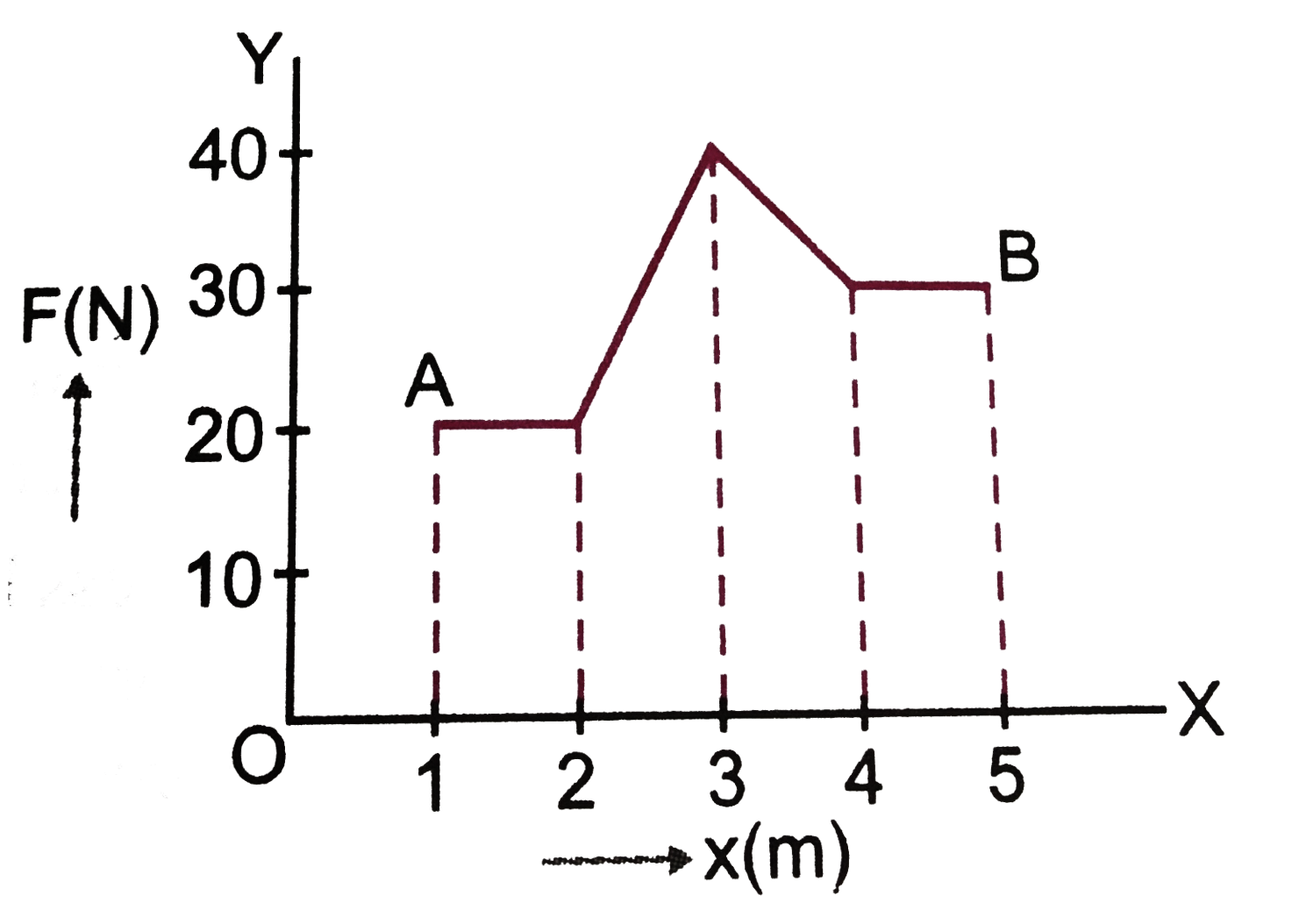
View SolutionA body moves from a point A to B under the action of a force shown in figure. What is the amount of work done ?
View SolutionCalculate the work done by the force →F=yˆi to move the particle from (0,0) to (1,1) in the following condition
(a) y = x (b) y = x2
View SolutionOn applying a force (→F=3ˆi−6ˆj+4ˆk) N on a body , the body is dispalced through along negative direction of X - axis is 2 m . Calculate the work done by this force .
View SolutionA body of mass 1kg begins to move under the action of a time dependent force →F=(2tˆi+3t2ˆj)N, where ˆi and ˆj are unit vectors along X and Y axis. What does will be developed by the source at time t ?
View Solution
