A body of mass 1kg begins to move under the action of a time dependent force →F=(2tˆi+3t2ˆj)N, where ˆi and ˆj are unit vectors along X and Y axis. What does will be developed by the source at time t ?
(2t2+4r4)W
(2t2+3r4)W
(2t3+3r5)W
(2t+3r3)W
The correct Answer is:C
To solve the problem, we need to determine the power developed by a body of mass 1 kg under the influence of a time-dependent force given by →F=(2t^i+3t2^j)N.
1. Identify the Force and Mass:
The force acting on the body is:
→F=(2t^i+3t2^j)N
The mass of the body is:
m=1kg
2. Use Newton's Second Law:
According to Newton's second law, the force is equal to mass times acceleration:
→F=m→a
Since m=1kg, we have:
→a=→F=(2t^i+3t2^j)m/s2
3. Find the Velocity:
The acceleration is the time derivative of velocity:
→a=d→vdt
Thus, we can write:
d→vdt=(2t^i+3t2^j)
Integrating both sides with respect to time t:
→v=∫(2t^i+3t2^j)dt
Performing the integration:
→v=(t2^i+t3^j)+→C
Assuming the initial velocity is zero (the body starts from rest), we have:
→C=0⇒→v=t2^i+t3^j
4. Calculate Power:
Power P developed by the force is given by the dot product of the force and velocity:
P=→F⋅→v
Substituting the expressions for →F and →v:
P=(2t^i+3t2^j)⋅(t2^i+t3^j)
Calculating the dot product:
P=2t⋅t2+3t2⋅t3=2t3+3t5
5. Final Result:
Therefore, the power developed by the body at time t is:
P(t)=2t3+3t5W
The force acting on the body is:
→F=(2t^i+3t2^j)N
The mass of the body is:
m=1kg
According to Newton's second law, the force is equal to mass times acceleration:
→F=m→a
Since m=1kg, we have:
→a=→F=(2t^i+3t2^j)m/s2
The acceleration is the time derivative of velocity:
→a=d→vdt
Thus, we can write:
d→vdt=(2t^i+3t2^j)
Integrating both sides with respect to time t:
→v=∫(2t^i+3t2^j)dt
Performing the integration:
→v=(t2^i+t3^j)+→C
Assuming the initial velocity is zero (the body starts from rest), we have:
→C=0⇒→v=t2^i+t3^j
Power P developed by the force is given by the dot product of the force and velocity:
P=→F⋅→v
Substituting the expressions for →F and →v:
P=(2t^i+3t2^j)⋅(t2^i+t3^j)
Calculating the dot product:
P=2t⋅t2+3t2⋅t3=2t3+3t5
Therefore, the power developed by the body at time t is:
P(t)=2t3+3t5W
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Comprehension
9 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Integer Type Questions
9 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - NCERT( Multiple choide questions-1)
21 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
A body constrainedto move along the z-axis of a co-ordinate system is subjected to a constant force →F given by →F=−ˆi+2ˆj+3ˆk newton where ˆi,ˆjand ˆk represent unit vectors along x-,y-,and z-axes of the system, respectively.Calculate the work done by this force in displacing the body through a distance of 4malong the z-axis.
View SolutionIf ˆiandˆj are unit vectors along X- and Y-axis respectively, then what is the magnitude and direction of ˆi+ˆjandˆi−ˆj ?
View Solution
Knowledge Check
A body of mass 1 kg begins to move under the action of a time dependent force F=(2tˆi+3t2ˆj)N,whereˆiandˆj are unit vector along x and y axis. What power will be developed by the force at the time?
A(2t3+3t4)WB(2t3+3t5)WC(2t2+3t2)WD(2t2+3t4)WA body of mass 1kg begins to move under the action of a time dependent force →F=(2tˆI+3t2ˆj)N, where ˆi and ˆj are unit vectors along x-and y-axes. What power will be developed by the force at the time t ?
A(2t2+3t3)WB(2t2+4t4)WC(2t3+3t4)WD(2t3+3t5)WThe angle which the vector →A=2ˆi+3ˆj makes with the y-axis, where ˆi and ˆj are unit vectors along x- and y-axis, respectively, is
Acos−1(3/5)Bcos−1(2/3)Ctan^(-1)(2//3)Dsin−1(2/3)
An object of mass 2 kg at rest at origin starts moving under the action of a force
→F=(3t2ˆi+4tˆj)N The velocity of the object at t = 2 s will be -
View SolutionThe unit vector along →A=2ˆi+3ˆj is :
View SolutionA particle of mass m moves from A to C under the action of force →F=2xyˆi+y2ˆj , along different paths as shown in figure.
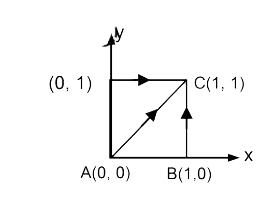
View SolutionIf →P=ˆi+ˆj−ˆk and →Q=ˆi−ˆj+ˆk, then unit vector along (→P−→Q) is :
View SolutionA particle of mass 2kg moves in the xy plane under the action of a constant force →F where →F=ˆi−ˆj. Initially the velocity of the particle is 2ˆj. The velocity of the particle at time t is
View Solution
