Uniform electrilcf and magnetic fields with strength E and B are directed along of x-axis. A particle with specific charge qm leves the origin in the direction of x-axis with an initial velocity v0. Find
a. the y-coordinate of the particle when it crosses the y-xis for nth time.
b. the angle α between the particle's velocity vector adn the y-axis for nth time
To solve the problem, we will break it down into two parts as per the question:
Part (a): Finding the y-coordinate of the particle when it crosses the y-axis for the nth time.
1. Understanding the Motion: The particle moves in a helical path due to the presence of uniform electric (E) and magnetic (B) fields. The helical path's axis is parallel to the y-axis.
2. Time to Cross the Y-axis: The time taken for the particle to cross the y-axis for the nth time can be expressed as:
Tn=2πmnqB
where n is the number of times the particle crosses the y-axis.
3. Acceleration in the y-direction: The acceleration in the y-direction (Ay) due to the electric field is given by:
Ay=qEm
4. Using the Kinematic Equation: Since the initial velocity in the y-direction is zero, we can use the kinematic equation for displacement:
y=12AyT2n
5. Substituting Values: Substitute Ay and Tn into the equation:
y=12(qEm)(2πmnqB)2
6. Simplifying the Expression: Simplifying the above expression gives:
y=2n2mEπ2qB2
Part (b): Finding the angle α between the particle's velocity vector and the y-axis for the nth time.
1. Finding the y-component of Velocity: The y-component of the velocity (Vy) can be calculated as:
Vy=AyTn=(qEm)(2πmnqB)
2. Simplifying Vy: This simplifies to:
Vy=2πnEB
3. Finding the Velocity in the XZ Plane: The velocity in the XZ plane (Vxz) is equal to the initial velocity v0.
4. Calculating the Angle α: The angle α can be found using the tangent function:
tan(α)=VxzVy=v02πnEB
5. Final Expression for Angle: Thus, the angle α is given by:
α=tan−1(v0B2πnE)
Summary of Results:
- The y-coordinate of the particle when it crosses the y-axis for the nth time is:
y=2n2mEπ2qB2
- The angle α between the particle's velocity vector and the y-axis for the nth time is:
α=tan−1(v0B2πnE)
Tn=2πmnqB
where n is the number of times the particle crosses the y-axis.
Ay=qEm
y=12AyT2n
y=12(qEm)(2πmnqB)2
y=2n2mEπ2qB2
Vy=AyTn=(qEm)(2πmnqB)
Vy=2πnEB
tan(α)=VxzVy=v02πnEB
α=tan−1(v0B2πnE)
- The y-coordinate of the particle when it crosses the y-axis for the nth time is:
y=2n2mEπ2qB2
- The angle α between the particle's velocity vector and the y-axis for the nth time is:
α=tan−1(v0B2πnE)
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
Uniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q/m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v0

The coordinate yn of the particle when it crosses the y-axis for the nth time is
View SolutionUniform electric field E and magnetic field B, respectively, are along y-axis as shown in the figure. A particle with specific charge q/m leaves the origin O in the direction of x-axis with an initial non-relativistic speed v0.Thec∞rd∈ateY_(n) of the particle when it crosses the y-axis for the nth time is:
View SolutionUniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q/m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v0

The angle α between the particle's velocity vector and y-axis at and moment is
View SolutionA charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionA particle of mass m and charge q is lying at the origin in a uniform magnetic field B directed along x-axis. At time t = 0, it is given a velocity v0, at an angleθ with the y-axis in the xy-plane. Find the coordinates of the particle after one revolution.
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View SolutionA particle of specific charge alpha enters a uniform magnetic field B=−B0ˆk with velocity v=v0ˆi from the origin. Find the time dependence of velocity and position of the particle.

View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
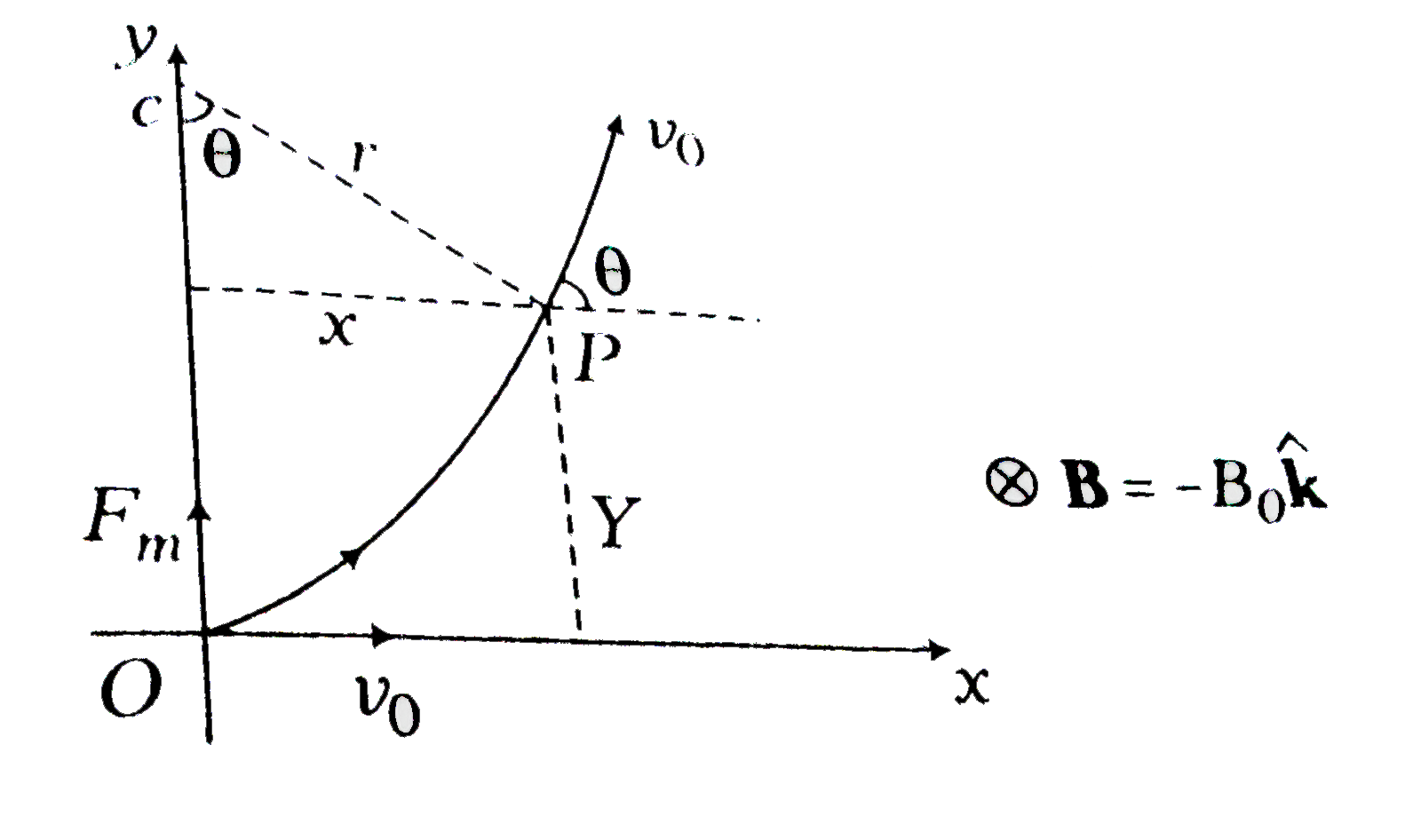
View Solution
