Uniform electric field E and magnetic field B, respectively, are along y-axis as shown in the figure. A particle with specific charge q/m leaves the origin O in the direction of x-axis with an initial non-relativistic speed v0.Thec∞rd∈ateY_(n) of the particle when it crosses the y-axis for the nth time is:
2π2mn2EqB2
π2mn2EqB2
2π2mn2E3qB2
√3π2mn2EqB2
The correct Answer is:A
To solve the problem, we need to determine the coordinate Yn of a particle when it crosses the y-axis for the nth time, given that it is subjected to uniform electric and magnetic fields.
1. Identify Forces Acting on the Particle:
The particle experiences two forces:
- Due to the electric field E, the force is FE=qE.
- Due to the magnetic field B, the force is FB=q(v×B). However, since the particle moves along the x-axis initially, we will focus on the electric force for vertical motion.
2. Calculate Acceleration:
The acceleration a of the particle in the y-direction due to the electric field is given by:
a=FEm=qEm
3. Determine the Time Period for Circular Motion:
The particle will undergo circular motion in the x-z plane due to the magnetic field. The time period T for one complete revolution in the x-z plane is:
T=2πmqB
4. Calculate Total Time for n Revolutions:
For n revolutions, the total time t is:
t=nT=n⋅2πmqB
5. Calculate the Displacement in y-direction:
The displacement Yn in the y-direction when the particle crosses the y-axis for the nth time can be calculated using the equation of motion:
Yn=12at2
Substituting the values of a and t:
Yn=12(qEm)(n⋅2πmqB)2
6. Simplify the Expression:
Now, simplifying the expression:
Yn=12⋅qEm⋅(n2⋅4π2m2q2B2)
Yn=2π2mn2EqB2
Final Result:
Thus, the coordinate Yn of the particle when it crosses the y-axis for the nth time is:
Yn=2π2mn2EqB2
The particle experiences two forces:
- Due to the electric field E, the force is FE=qE.
- Due to the magnetic field B, the force is FB=q(v×B). However, since the particle moves along the x-axis initially, we will focus on the electric force for vertical motion.
The acceleration a of the particle in the y-direction due to the electric field is given by:
a=FEm=qEm
The particle will undergo circular motion in the x-z plane due to the magnetic field. The time period T for one complete revolution in the x-z plane is:
T=2πmqB
For n revolutions, the total time t is:
t=nT=n⋅2πmqB
The displacement Yn in the y-direction when the particle crosses the y-axis for the nth time can be calculated using the equation of motion:
Yn=12at2
Substituting the values of a and t:
Yn=12(qEm)(n⋅2πmqB)2
Now, simplifying the expression:
Yn=12⋅qEm⋅(n2⋅4π2m2q2B2)
Yn=2π2mn2EqB2
Thus, the coordinate Yn of the particle when it crosses the y-axis for the nth time is:
Yn=2π2mn2EqB2
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Main (Archive)
Explore 75 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Advanced (Archive)
Explore 78 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:LEVEL 1
Explore 75 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE ADVANCED (LEVEL -2)
Explore 55 Videos
- MOCK TEST 1Book:VMC MODULES ENGLISHChapter:MOCK TEST 1Exercise:PART I : PHYSICS (SECTION-2)
Explore 10 Videos
Similar Questions
Uniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q/m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v0

The coordinate yn of the particle when it crosses the y-axis for the nth time is
View SolutionUniform electric and magnetic fields with strength E and induction B, respectively, are along y-axis as shown in Fig. A particle with specific charge q/m leaves the origin O in the direcction of x-axis with an initial non-relativistic velocity v0

The angle α between the particle's velocity vector and y-axis at and moment is
View SolutionUniform electrilcf and magnetic fields with strength E and B are directed along of x-axis. A particle with specific charge qm leves the origin in the direction of x-axis with an initial velocity v0. Find
a. the y-coordinate of the particle when it crosses the y-xis for nth time.
b. the angle α between the particle's velocity vector adn the y-axis for nth time
View SolutionA uniform electric field of 400Vm is directed at 45∘ above the x-axis as shown in the figure. The potential difference VA−VB is given by
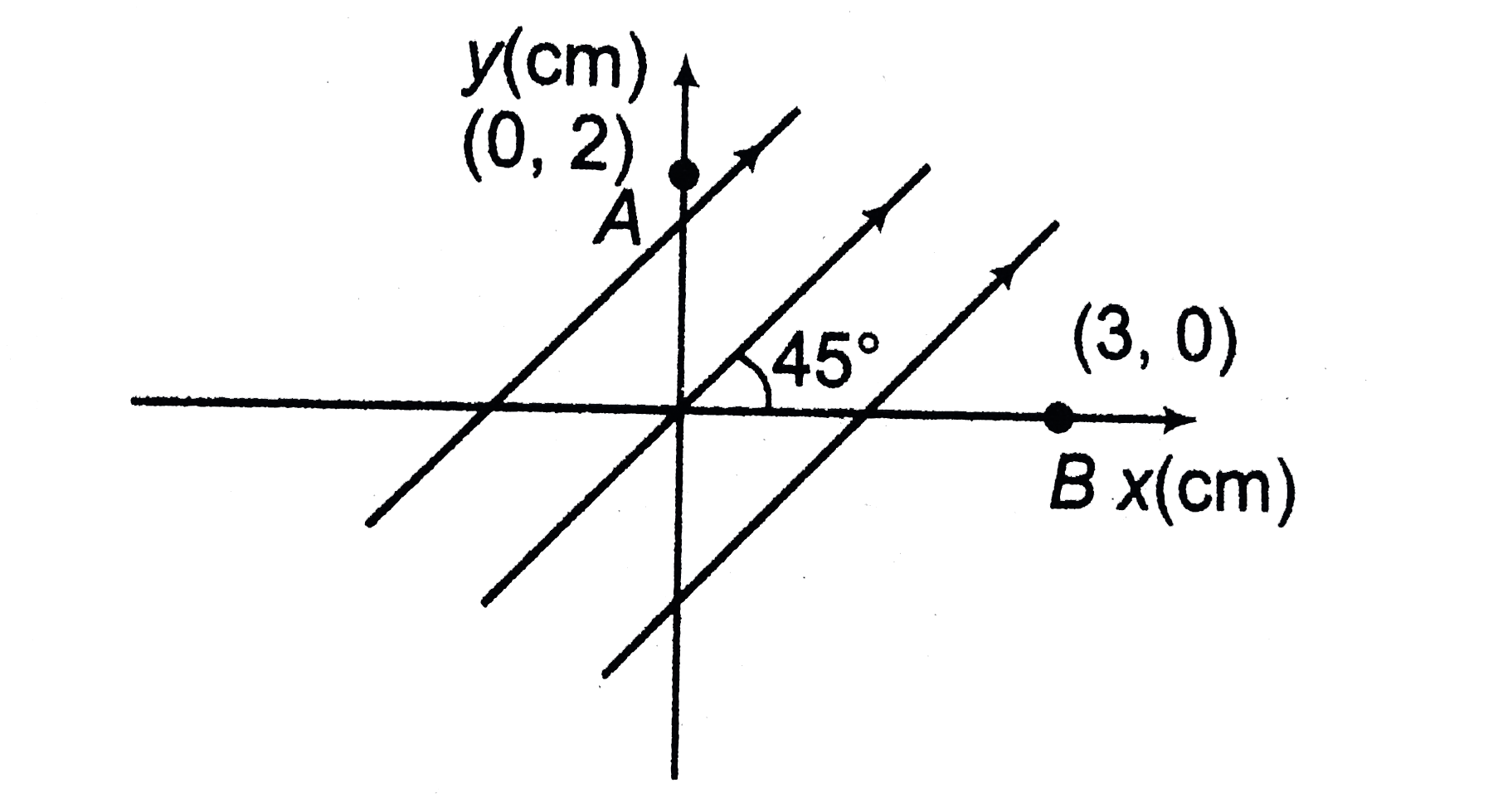
View SolutionA charged particle (charge q, mass m) has velocity v0 at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionA uniform electric field of 400V/m is directed at 45∘ to the positive X-axis, in the X−Y plane as shown in figure

View SolutionA non-uniform magnetic field →B=B0(1+yd)(−ˆk) is present in region of space in between y=0&y=d.The lines are shown in the diagram.A particle of mass m and positive charge q is moving.Given an initial velocity →v=v0ˆi.Find the components of velocity of the particle when it leaves the field.
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic. field of strength B is also switched on along positive y-axis.
x-coordinate of the particle as a function of time after the magnetic field is switched on is
View Solution