Question

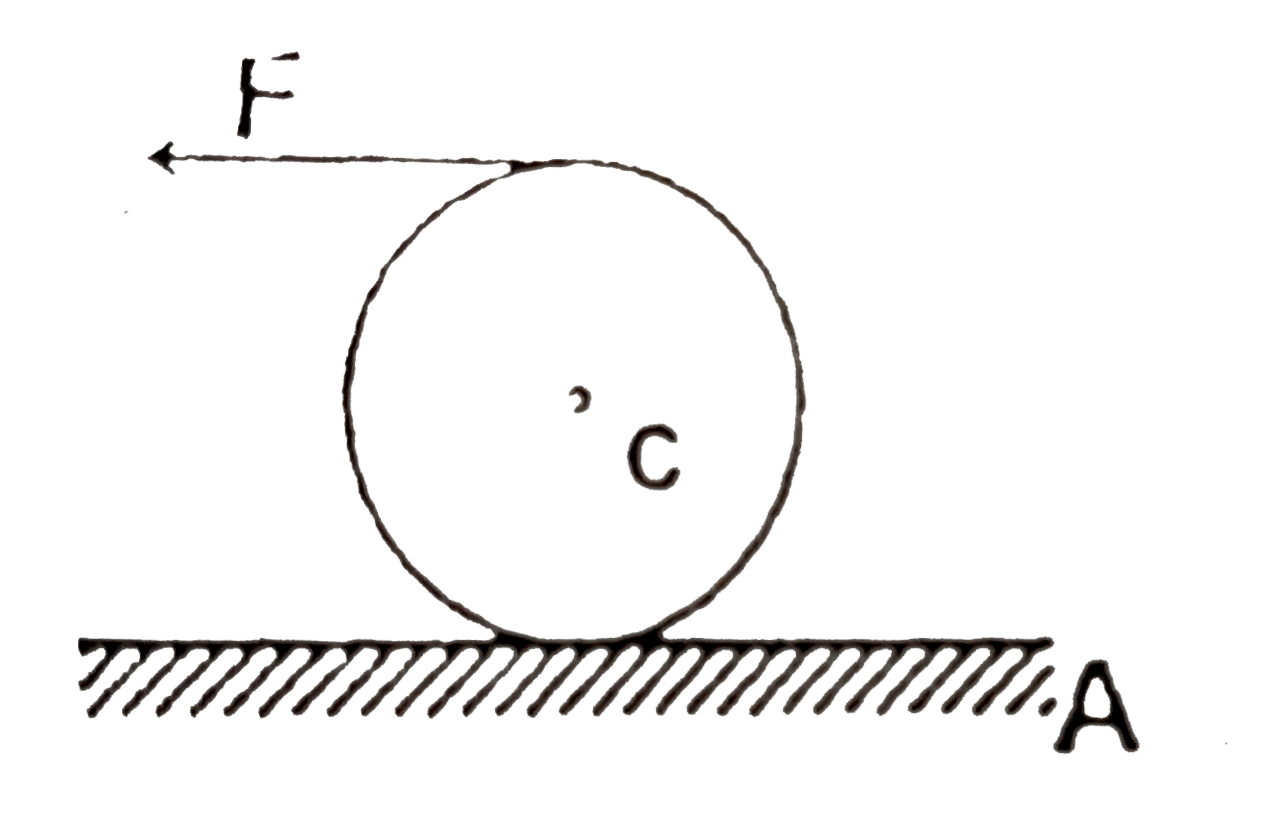
Uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force is applied at the top point P of the cylinder so that it start pure rolling .In the above question, the frictional force on the cylinder is

Options

A. `F//3` towards right
B. `F//3` towards left
C. `2F//3` towards right
D. `2F//3` towards left

Explanation

To solve the problem of finding the frictional force acting on a uniform solid cylinder of mass $$m$$ and radius $$R$$ when a horizontal constant force $$F$$ is applied at the top point $$P$$ of the cylinder, we can follow these steps:

Step 1: Understand the System
We have a uniform solid cylinder placed on a rough horizontal surface. A horizontal force \( F \) is applied at the top of the cylinder, and we need to find the frictional force acting on it when it starts pure rolling.

Step 2: Identify Forces Acting on the Cylinder
1. The applied force \( F \) acts horizontally at the top point \( P \).
2. The frictional force \( f \) acts at the point of contact with the ground, opposing the motion.
3. The weight of the cylinder \( mg \) acts downward at its center of mass.
4. The normal force \( N \) acts upward at the point of contact.

Step 3: Write the Equation of Motion
Using Newton's second law for translational motion:
\( F - f = ma \quad (1) \)
where \( a \) is the linear acceleration of the center of mass of the cylinder.

Step 4: Write the Torque Equation
The torque \( \tau \) about the center of mass due to the applied force \( F \) and the frictional force \( f \) is given by:
\( \tau = F \cdot R - f \cdot R = I \alpha \quad (2) \)
where \( I \) is the moment of inertia of the cylinder and \( \alpha \) is the angular acceleration.

For a solid cylinder, the moment of inertia \( I \) is:
\( I = \frac{1}{2} m R^2 \)

Step 5: Relate Linear and Angular Acceleration
For pure rolling motion, the relationship between linear acceleration \( a \) and angular acceleration \( \alpha \) is:
\( a = \alpha R \quad (3) \)

Step 6: Substitute \( \alpha \) in the Torque Equation
From equation (2), substituting \( \alpha \) using equation (3):
\( F \cdot R - f \cdot R = \frac{1}{2} m R^2 \cdot \frac{a}{R} \)
Simplifying gives:
\( F - f = \frac{1}{2} ma \quad (4) \)

Step 7: Solve the System of Equations
Now we have two equations:
1. \( F - f = ma \) (equation 1)
2. \( F - f = \frac{1}{2} ma \) (equation 4)

Setting these equal to each other:
\( ma = \frac{1}{2} ma \)
Subtracting gives:
\( \frac{1}{2} ma = f \)
Thus, we can express \( f \):
\( f = \frac{1}{2} ma \)

Step 8: Substitute \( a \) from Equation (1)
From equation (1):
\( f = F - ma \)
Substituting \( a \) from \( f = \frac{1}{2} ma \):
\( f = F - 2f \)
Rearranging gives:
\( 3f = F \quad \Rightarrow \quad f = \frac{F}{3} \)

Final Answer
The frictional force \( f \) acting on the cylinder is:
\( f = \frac{F}{3} \)