Values of the acceleration A of a particle moving in simple harmonic motion as a function of its displacement x are given in the table below.
∣∣∣A(mms−2)1680−8−16x(mm)−4−2024∣∣∣
The pariod of the motion is
1πs
2πs
π2s
πs
The correct Answer is:D
Step by step video, text & image solution for Values of the acceleration A of a particle moving in simple harmonic motion as a function of its displacement x are given in the table below. |{:(A(mm s^(-2)),16,8,0,-8,-16),(x(mm),-4,-2,0,2,4):}| The pariod of the motion is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason
23 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
- SURFACE TENSIONBOOK - ERRORLESS CHAPTER - SURFACE TENSIONEXERCISE - Exercise
214 Videos
Similar Questions
Knowledge Check
Value of the acceleration A of a particle moving in sample harmonic motion as a function of its displacement x are given in the table below .
A(mm s−2) 16 8 0 −8 −16
x(mm) −4 −2 0 2 4
The period of the motion isA1πsB2πsCπ2sDπsIf the period of oscillation of particle performing simple harmonic motion is 8 s, than the frequency of its kinetic energy will be
A0.5s−1B0.25s−1C1s−1D2s−1The x−t graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at t=4/3s is
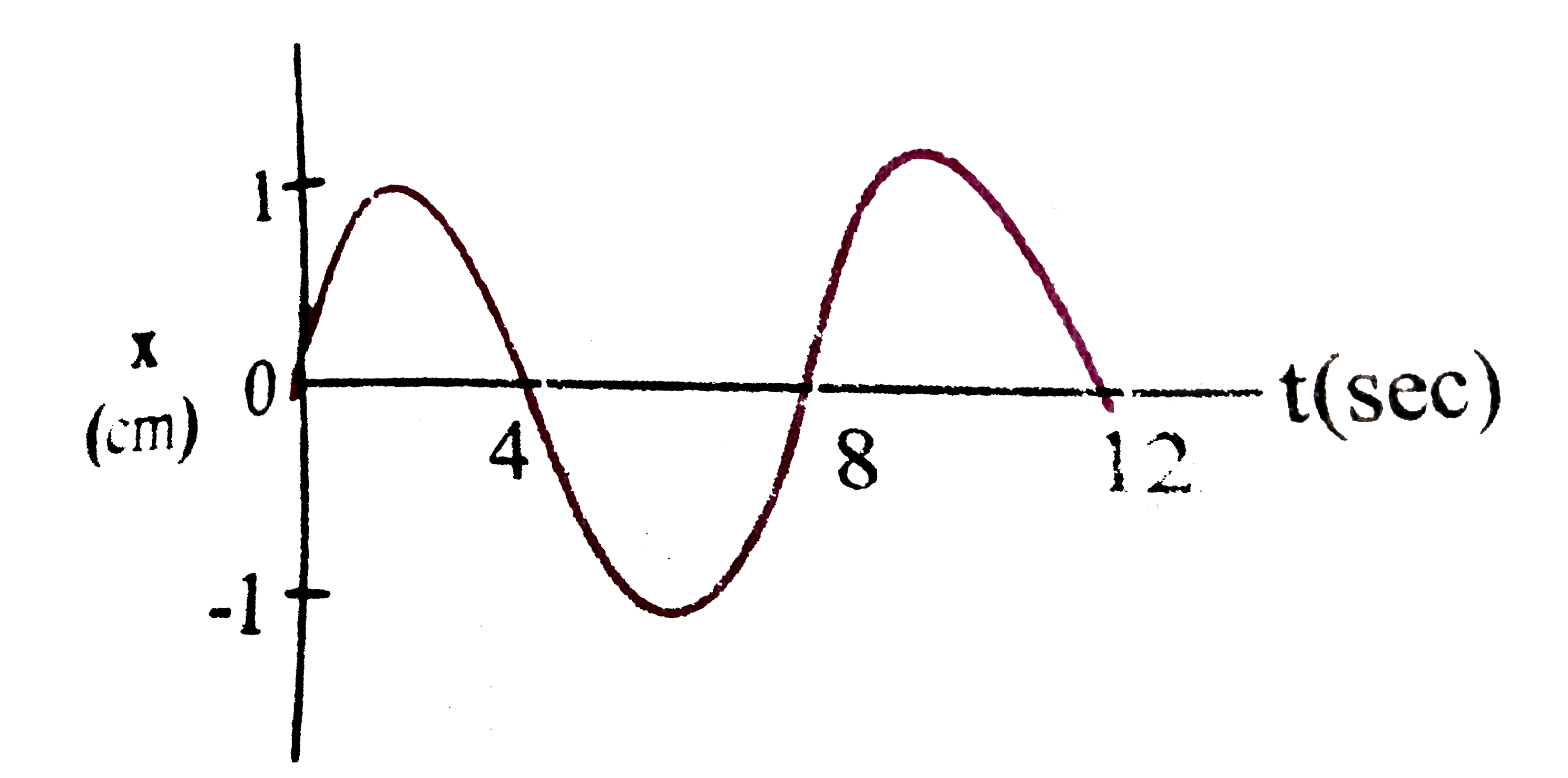 A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
A√332π2cm/s2B−π232cm/s2Cπ232cm/s2D−√332π2cm/s2
The acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.

View SolutionMaximum acceleration of an object in simple harmonic motion is 24m/s^(2) and maximum velocity is 16m/ sec. The amplitude of object is
View SolutionThe x−t graph of a particle undergoing simple harmonic motion is shown below. The accelertion of the particle at t=4/3s is
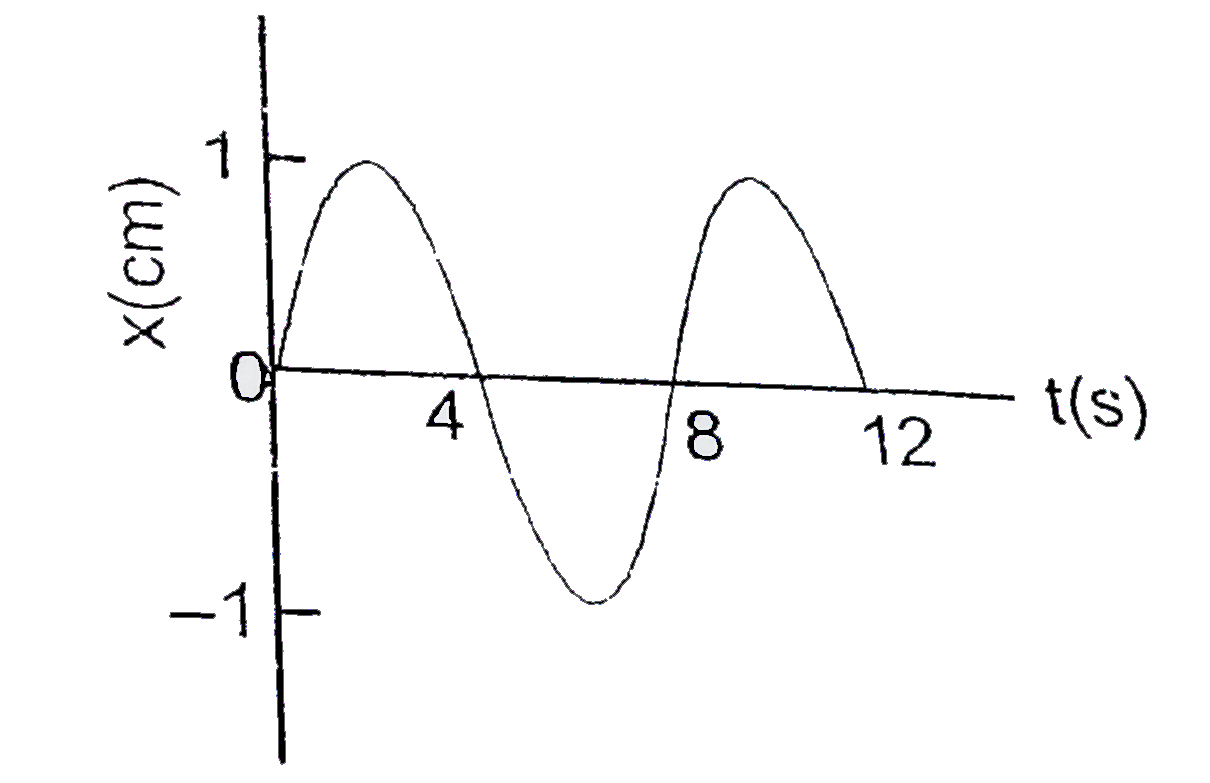
View SolutionThe x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle of t=4/3s is

View SolutionThe equation of S.H.M. of a particle is a+4π2x=0, where a is instantaneous linear acceleration at displacement x. Then the frequency of motion is
View Solution

