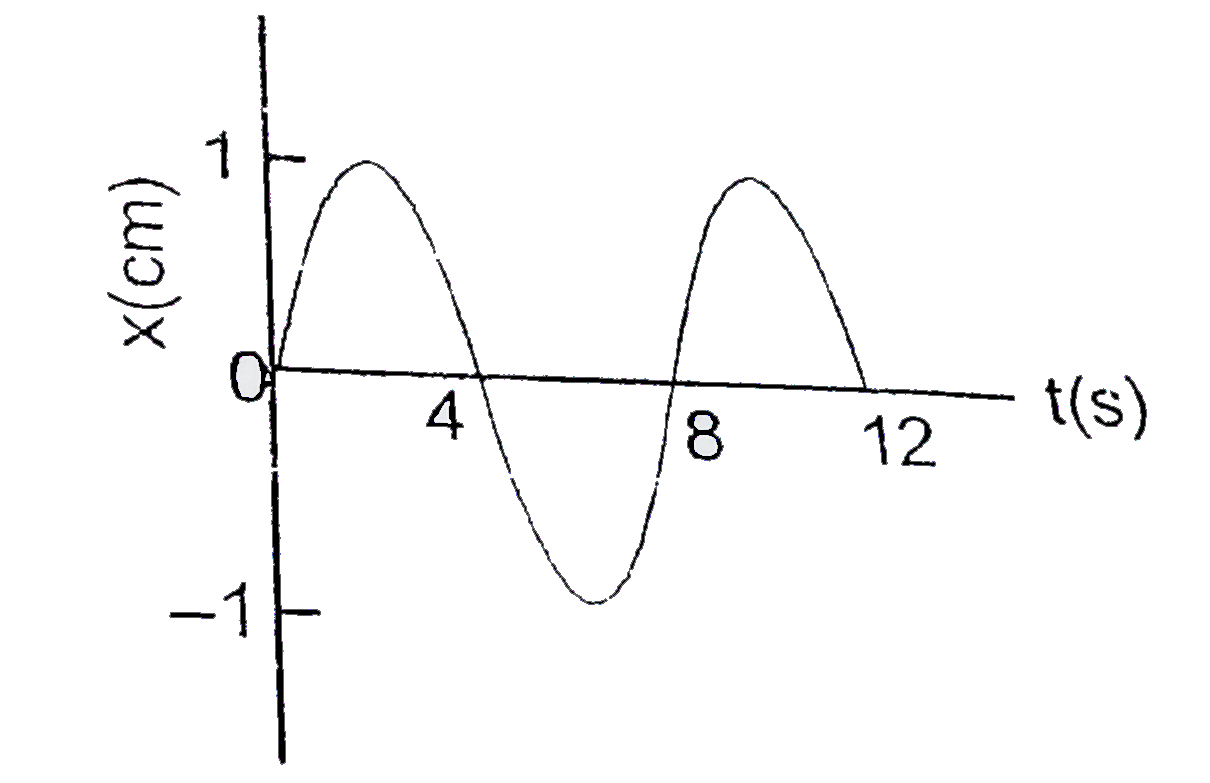
The $x - t$ graph of a particle undergoing simple harmonic motion is shown below. The accelertion of the particle at $t = 4 / 3 s$ is

A

$\frac{\sqrt{3}}{32} π^{2} c m / s^{2}$

B

$\frac{- π^{2}}{32} c m / s^{2}$

C

$\frac{π^{2}}{32} c m / s^{2}$

D

$- \frac{\sqrt{3}}{32} π^{2} c m / s^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

From graph
$T = 8$ second, $A = 1 c m, x = A sin ω t . = 1 \frac{sin (2 π)}{8} t$ .
$a = - ω^{2} x = - {(\frac{2 π}{8})}^{2} sin (\frac{2 π}{8}) t c m / s^{2}$
At, $t = \frac{4}{3}$ second, $a = - {(\frac{2 π}{8})}^{2} sin \frac{π}{3} = - \frac{\sqrt{3} π^{2}}{32} c m / s^{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle of $t = 4 / 3 s$ is

A $\frac{\sqrt{3}}{32} π^{2} c m / s^{2}$
B $\frac{- π^{2}}{32} c m / s^{2}$
C $\frac{π^{2}}{32} c m / s^{2}$
D $- \frac{\sqrt{3}}{32} π^{2} c m / s^{2}$
Question 2 - Select One
The $x - t$ graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at $t = 4 / 3 s$ is

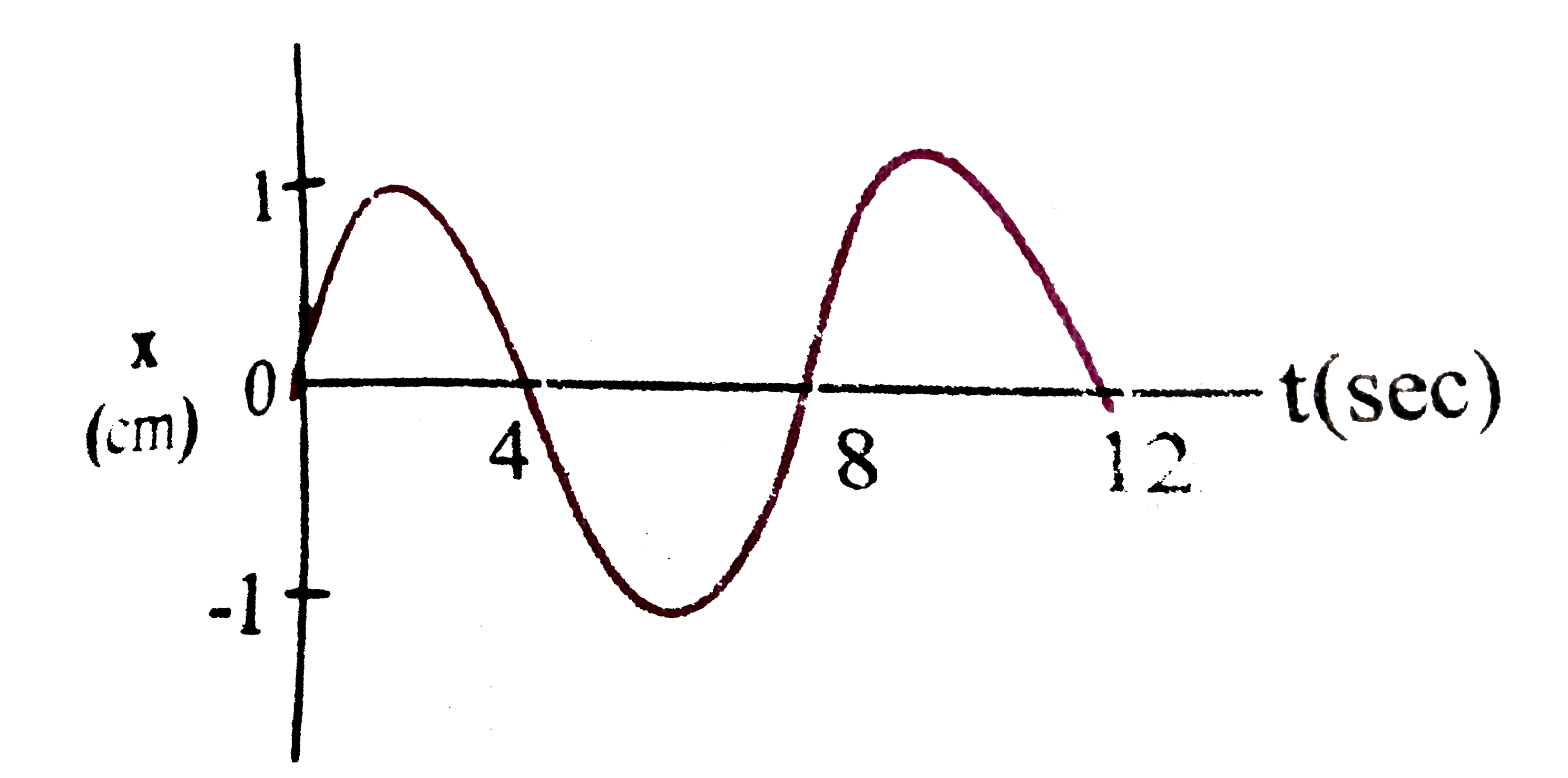A $\frac{\sqrt{3}}{32} π^{2} c m / s^{2}$
B $\frac{- π^{2}}{32} c m / s^{2}$
C $\frac{π^{2}}{32} c m / s^{2}$
D $- \frac{\sqrt{3}}{32} π^{2} c m / s^{2}$
Question 3 - Select One
The x-t graph of a particle undergoing SHM is as shown in figure. The acceleration of the particle at $t = 2 / 3$ is

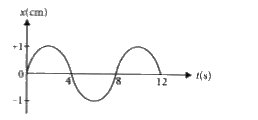A $\frac{\sqrt{3}}{32} π^{2} c m s^{- 2}$
B $- \frac{π^{2}}{32} c m s^{- 2}$
C $\frac{π^{2}}{32} c m s^{- 2}$
D $- \frac{\sqrt{3}}{32} π^{2} c m s^{- 2}$

RESONANCE-SIMPLE HARMONIC MOTION -Exercise- 3, PART - I

Home
Ask Doubt
Profile