Vertical displacement of a plank with a body of mass m on it is varying according to the law y=sinωt+√3cosωt. The minimum value of ω for which the mass just breaks off the plank and the moment it occurs first time after t=0, are given by (y is positive towards vertically upwards).
√g2,√26,π√g
g√2,23√πg)
√g2,π3)√2g
√2g,√2π3g
The correct Answer is:A
To solve the problem, we need to analyze the vertical displacement of the plank with the mass on it, given by the equation:
y=sin(ωt)+√3cos(ωt)
Step 1: Rewrite the equation in a standard form
We can express the equation in a more recognizable form by combining the sine and cosine terms. We can use the identity for sine of a sum:
y=Asin(ωt+ϕ)
where A is the amplitude and ϕ is the phase angle. To find A and ϕ, we calculate:
- A=√12+(√3)2=√1+3=√4=2
- tan(ϕ)=coefficient of sincoefficient of cos=1√3⇒ϕ=30∘ or π6 radians.
Thus, we can rewrite the equation as:
y=2sin(ωt+π6)
Step 2: Determine the conditions for the mass to lose contact with the plank
The mass will lose contact with the plank when the normal force N becomes zero. The forces acting on the mass are:
- Weight mg acting downwards.
- Normal force N acting upwards.
Using Newton's second law, we have:
N−mg=ma
where a is the acceleration of the mass. When the mass just loses contact, N=0, thus:
−mg=ma
a=−g
Step 3: Relate acceleration to the motion of the plank
The acceleration a of the mass is given by the second derivative of the displacement y:
a=d2ydt2=−ω2y
At the point of losing contact, we have:
−ω2y=−g
Substituting y at its maximum value (which is the amplitude A=2):
ω2⋅2=g
ω2=g2
ω=√g2
Step 4: Calculate the minimum value of ω
Using g≈9.8m/s2:
ω=√9.82=√4.9≈2.21rad/s
Step 5: Determine the time when the mass first loses contact
To find the time t when the mass first loses contact, we set y equal to the maximum amplitude:
y=2sin(ωt+π6)=2
This occurs when:
sin(ωt+π6)=1
The first occurrence of this happens at:
ωt+π6=π2
ωt=π2−π6=3π6−π6=2π6=π3
Thus:
t=π/3ω=π/3√4.9
Calculating t:
t≈1.0472.21≈0.474s
Final Answers
- The minimum value of ω is approximately 2.21rad/s.
- The time t when the mass first loses contact is approximately 0.474s.
We can express the equation in a more recognizable form by combining the sine and cosine terms. We can use the identity for sine of a sum:
- tan(ϕ)=coefficient of sincoefficient of cos=1√3⇒ϕ=30∘ or π6 radians.
The mass will lose contact with the plank when the normal force N becomes zero. The forces acting on the mass are:
- Normal force N acting upwards.
a=−g
The acceleration a of the mass is given by the second derivative of the displacement y:
ω2=g2
ω=√g2
Using g≈9.8m/s2:
To find the time t when the mass first loses contact, we set y equal to the maximum amplitude:
ωt=π2−π6=3π6−π6=2π6=π3
- The minimum value of ω is approximately 2.21rad/s.
- The time t when the mass first loses contact is approximately 0.474s.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:More than one option is correct
Explore 50 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Comprehension types
Explore 18 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEYChapter:SIMPLE HARMONIC MOTIONExercise:Only one question is correct
Explore 48 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEYChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEYChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
A horizontal plane supports a plank with a bar of mass m placed on it and attached by a light elastic non-deformed cord of length l0, to a point O. The coefficient of friciton between the bar and the plank is equal to m. The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord derivates from the vertical by an angle θ.
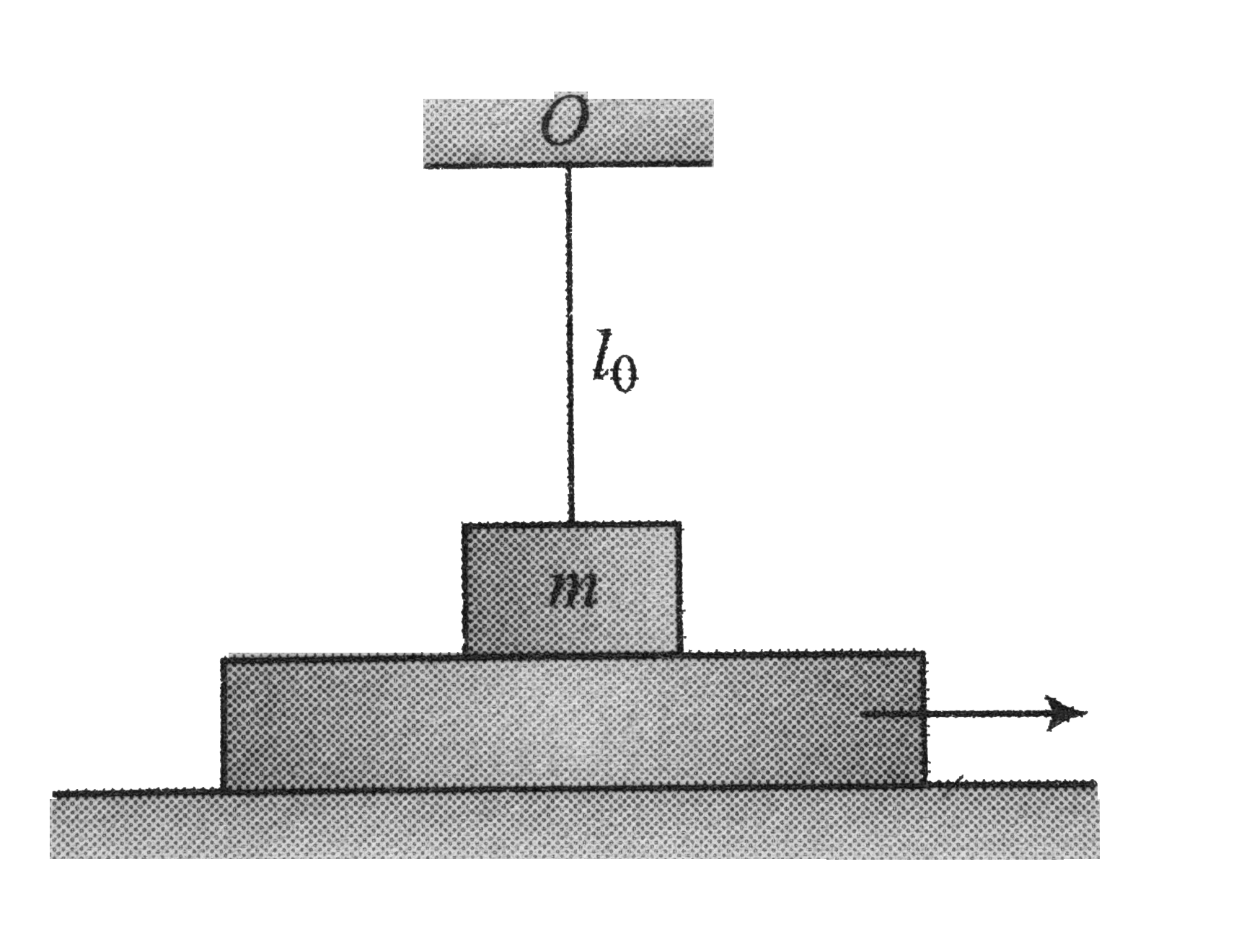
Find the work that has been performed by the moment by the frictional force acting on the bar in the reference frame fixed to the plane.
View SolutionA particle of mass 'm' is moving in the x−y plane such that its x and y coordinate very according to the law x=asinωt and y=acosωt where 'a' and 'ω' are positive constants and 't' is time. Find
(a) equation of the path. Name the trajectory (path)
(b) whether the particle moves in clockwise or anticlockwise direction
magnitude of the force on the particle at any time t.
View Solution
Knowledge Check
Vertical displacement of a plank with a body of mass 'm' on it is varying according to law y=sinωt+√3cosωt. The minium value of ω for which the mass just breaks off the plank and the moment it occurs first arter t=0 are given by: (yis positive vertically upwards)
A√g2,√26π√gBg√2,23√πgC√g2,π3√2gD√2g,√2π3gVertical displacement of a plank with a body of mass 'm' on it is varying according to law y=sinωt+√3cosωt. The minimum value of ω for which the mass just breaks off the plank and the moment it occurs first after t=0 are given by: (yis positive vertically upwards)
A√g/2,√26π√gBg√2,23√π/gC√g/2,π3√2/gD√2g,√2π/3gA thin non conducting ring of mass m, radius a carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment, the ring was at rest in horizontal position and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law B=B0t. Neglecting magnetism induced due to rotational motion of ring.
Find intantaneous power developed by electric force acting on the ring at t=1sA2q2B20a214mBq2B20a28mC3q2B20a2mDq2B20a24m
A particle of mass 'm' is moving in the x-y plane such that its x and y coordinate vary according to the law x= a sin ωt and y= a cos ωt where 'a' and 'omega' are positive constants and 't' is time. Find
(a) equation of the path. Name the trajectory (path).
(b) whether the particle moves in clockwise or anticlockwise direction
(c) magnitude of the force on the particle at any time t.
View SolutionA plank with a body of mass m placed on it starts moving straight up according to the law y=a(1−cosωt), where y is the displacement from the initial position, ω=11rad/s. Find
(a) The time independence of the force that the body exerts on the plank.
(b) The minimum amplitude of oscillations of the plank at which the body starts falling behind the plank.
View SolutionThe position of a particle moving along x-axis varies with time t according to equation x=√3sinωt−cosωt where ω is constants. Find the refion in which the particle is confined.
View SolutionA thin non conducting ring of mass m, radius a carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment, the ring was at rest in horizontal position and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law B=B0t. Neglecting magnetism induced due to rotational motion of ring.
The magnitude of an electric field on the circumference of the ring is
View SolutionA thin non conducting ring of mass m, radius a carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment, the ring was at rest in horizontal position and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law B=B0t. Neglecting magnetism induced due to rotational motion of ring.
Angular acceleration of ring is
View Solution