Water is flowing at a speed of 1.5ms−1 through a horizontal tube of cross-sectional area 10−2m2 and you are trying to stop the flow by your palm. Assuming that the water stops immediately after hitting the palm, the minimum force that you must exert should be (density of water = 103kgm−3).
15 N
22.5 N
33.7 N
45 N
The correct Answer is:B
To solve the problem of determining the minimum force required to stop the flow of water with a given speed, we can follow these steps:
Step 1: Identify the initial and final velocities of the water.
- The initial velocity v1 of the water is given as 1.5m/s.
- The final velocity v2 after hitting the palm is 0m/s.
Step 2: Calculate the change in velocity (Δv).
Δv=v1−v2=1.5m/s−0m/s=1.5m/s
Step 3: Calculate the mass of water flowing per unit time.
To find the mass of water flowing through the tube, we need to use the formula:
Mass=Density×Volume
The volume of water flowing through the tube per second can be calculated using the cross-sectional area and the velocity:
Volume per second=Area×Velocity=A×v1
Given:
- Area A=10−2m2
- Density ρ=103kg/m3
Calculating the volume:
Volume=10−2m2×1.5m/s=1.5×10−2m3/s
Now, calculating the mass of water flowing per second:
Mass=ρ×Volume=103kg/m3×1.5×10−2m3/s=15kg/s
Step 4: Calculate the force using the formula F=m⋅a.
We can use the formula for force:
F=m⋅ΔvΔt
Assuming the time interval Δt=1s for simplicity:
F=15kg/s⋅1.5m/s1s=15N
Final Answer:
The minimum force that you must exert to stop the flow of water is 15N.
---
- The initial velocity v1 of the water is given as 1.5m/s.
- The final velocity v2 after hitting the palm is 0m/s.
Δv=v1−v2=1.5m/s−0m/s=1.5m/s
To find the mass of water flowing through the tube, we need to use the formula:
Mass=Density×Volume
The volume of water flowing through the tube per second can be calculated using the cross-sectional area and the velocity:
Volume per second=Area×Velocity=A×v1
Given:
- Area A=10−2m2
- Density ρ=103kg/m3
Volume=10−2m2×1.5m/s=1.5×10−2m3/s
Mass=ρ×Volume=103kg/m3×1.5×10−2m3/s=15kg/s
We can use the formula for force:
F=m⋅ΔvΔt
Assuming the time interval Δt=1s for simplicity:
F=15kg/s⋅1.5m/s1s=15N
The minimum force that you must exert to stop the flow of water is 15N.
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
A stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall near by what is the force exerted on the wall by the impact of water assuming.that it does not rebound? (Density of water =1000kgm3)
View SolutionWater is moving with a speed of 5.18ms−1 through a pipe with a cross-sectional area of 4.20cm2. The water gradually descends 9.66m as the pipe increase in area to 7.60cm2. The speed of flow at the lower level is
View Solution
Knowledge Check
A stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water assuming that it does not rebound? (Density of water =1000kgm−3)
A1.25×103NB2.25×103NC3.25×103ND4.25×103NA stream of water flowing horizontally with a speed of 25ms−1 gushes out of a tube of cross-sectional area 10−3m2, and hits at a vertical wall nearby. What is the force exerted on the wall by the impact of water?
A125NB625NC−650ND−1125N
Water is flowing through a horizontal tube of non-uniform cross-section. At a place, the radius of the tube is 1.0cm and the velocity of water is 2m/s. What will be the velocity of water where the radius of the pipe is 2.0cm?
View SolutionWater flows steadily through a horizontal pipe of a variable cross-section. If the pressure of the water is p at a point , where the speed of the flow is v. What is the pressure at another point , where the speed of the flow is 2 v ? Let the density of water be 1gcm−3.
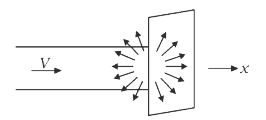
View SolutionA liquid of density ρ is flowing with a speed V through a pipe of cross sectional area A. What force does the liquid stream exert on wall in x direction if it splashes in the form of a circle after it hits the wall?
View SolutionCalculate the pressure due to a water column of height 100 m. (Take g=10ms−2 and density of water =103kgm−3).
View SolutionWater is flowing through a horizontal tube of length 0.25 m and radius 4×10−4 m under a constant pressure head of 0.2 m of water, at the rate of 5×10−6m3 per minutre . Calculate the coefficient of visosity of water. Density of water = 1000 kg m−3
View SolutionA horizontal pipeline carries water in a streamline flow. At a point along the pipe, where the cross- sectional area is 10cm2, the water velocity is 1ms−1 and the pressure is 2000 Pa. The pressure of water at another point where the cross-sectional area is 5cm2, is........Pa. (Density of water =103kg.m−3)
View Solution
