A projectile of mass M is fired so that the horizontal range is 4 km. At the highest point the projectile explodes in two parts of masses M/4 and 3M/4 respectively and the heavier part starts falling down vertically with zero initial speed. The horizontal range (distance form point of fring) of the lighter part is :
16km
1km
10km
2km
The correct Answer is:C
To solve the problem, we need to analyze the motion of the projectile and the effects of the explosion at its highest point. Here’s a step-by-step breakdown:
Step 1: Understand the initial conditions
The projectile is fired with a horizontal range of 4 km. This means that if the projectile were to continue its motion without any explosions, it would land 4 km away from the firing point.
Hint: Remember that the horizontal range is the total distance traveled horizontally before landing.
Step 2: Analyze the explosion
At the highest point of its trajectory, the projectile explodes into two parts: one with mass M4 (the lighter part) and the other with mass 3M4 (the heavier part). The heavier part falls vertically with zero initial speed.
Hint: The explosion does not affect the horizontal motion of the center of mass of the system.
Step 3: Apply the conservation of momentum
Since there are no external forces acting in the horizontal direction, the horizontal displacement of the center of mass remains unchanged. Thus, the horizontal range of the center of mass before and after the explosion is the same.
Hint: Use the principle of conservation of momentum to relate the masses and their respective displacements.
Step 4: Set up the equation for horizontal displacement
Let x1 be the horizontal range of the lighter part (M4) after the explosion. The heavier part (3M4) will not contribute to horizontal displacement since it falls straight down. The equation for the horizontal displacement of the center of mass can be written as:
M⋅R=(M4⋅x1)+(3M4⋅4)
Where R is the total horizontal range (4 km).
Hint: Factor out the mass M from the equation since it appears in all terms.
Step 5: Simplify the equation
Cancelling M from both sides gives:
4=14x1+3
Step 6: Solve for x1
Now, rearranging the equation to solve for x1:
4−3=14x1
1=14x1
Multiplying both sides by 4:
x1=4 km
Step 7: Conclusion
The horizontal range of the lighter part after the explosion is 4 km.
Final Answer: The horizontal range of the lighter part is 4 km.
The projectile is fired with a horizontal range of 4 km. This means that if the projectile were to continue its motion without any explosions, it would land 4 km away from the firing point.
At the highest point of its trajectory, the projectile explodes into two parts: one with mass M4 (the lighter part) and the other with mass 3M4 (the heavier part). The heavier part falls vertically with zero initial speed.
Since there are no external forces acting in the horizontal direction, the horizontal displacement of the center of mass remains unchanged. Thus, the horizontal range of the center of mass before and after the explosion is the same.
Let x1 be the horizontal range of the lighter part (M4) after the explosion. The heavier part (3M4) will not contribute to horizontal displacement since it falls straight down. The equation for the horizontal displacement of the center of mass can be written as:
Cancelling M from both sides gives:
Now, rearranging the equation to solve for x1:
The horizontal range of the lighter part after the explosion is 4 km.
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - MOTION IN A PLANE
87 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ATOMSBOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE
21 Videos
Similar Questions
A particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
(A)43R (B)32R (C)54R (D)2.5R
View SolutionA particle of mass 4m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 3m, respectively, such that the smaller mass comes to rest. The larger mass finally falls at a distance x from the point of projection, where x is equal to
View Solution
Knowledge Check
An object of mass 5 kg is projecte with a velocity of 20ms−1 at an angle of 60∘ to the horizontal. At the highest point of its path , the projectile explodes and breaks up into two fragments of masses 1kg and 4 kg. The fragments separate horizontally after the explosion, which releases internal energy such that K.E. of the system at the highest point is doubled. Calculate the separation betweent the two fragments when they reach the ground.
A11 mB22 mC44 mD66 mA projectile has a maximum range of 16 km. At the highest point of its motion, it explodes into two equal masses. One mass drops vertically downward. The horizontal distance covered by the other mass from the time of explosion
A8 kmB16 kmC24 kmD32 km
A projectile is fired at a speed of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Find the distance from the launching point to the where the heavier piece lands.
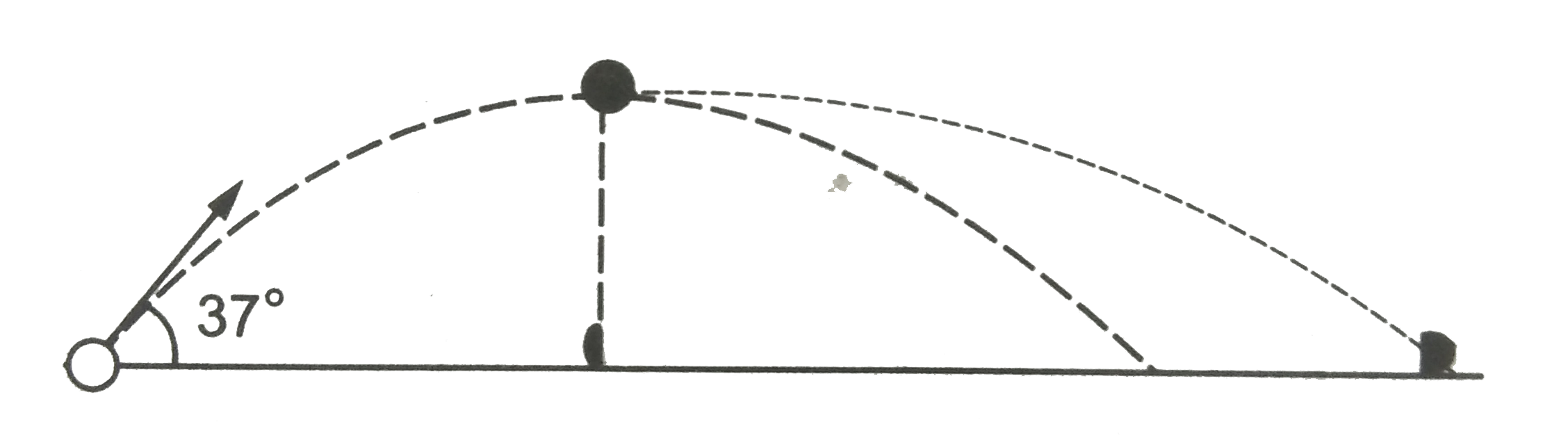
View SolutionA projectile is fired at a spedd of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Findthe distance from the launching point to the where the heavier piece lands.

View SolutionA projectile is fired with velocity u at an angle θ with horizontal. At the highest point of its trajectory, it splits up into three segments of masses m, m and 2m. First part falls vertically downward with zero initial velocity and second part returns via same path to the point of projection. The velocity of third part of mass 2 m just after explosion will be
View SolutionA body of mass m is projected from ground for horizontal range R. At the highest point it is fragmented into two identical parts. If one parts returns back to the point of projection, then other part will have the horizontal range
View SolutionA projectile of mass 3m is projected from ground with velocity 20√2m/s at 45∘. At highest point it explodes into two pieces. One of mass 2m and the other of mass m. Both the pieces fly off horizontally in opposite directions. Mass 2m falls at a distance of 100m from point of projection. Find the distance of second mass from point of projection where it strikes the ground.
(g=10m/s2)
View SolutionA projectile is fired from a gun at an angle of 45∘ with the horizontal and with a speed of 20m/s relative to ground. At the highest point in its flight the projectile explodes into two fragments of equal masses. One fragement, whose initial speed is zero falls vertically. How far from the gun does the other fragment land, assuming a level terrain? Take g=10m/s2?
View Solution
