Water is moving with a speed of 5.18ms−1 through a pipe with a cross-sectional area of 4.20cm2. The water gradually descends 9.66m as the pipe increase in area to 7.60cm2. The speed of flow at the lower level is
2.86ms−1
3.0ms−1
3.82ms−1
5.7ms−1
The correct Answer is:A
To solve the problem, we will use the principle of continuity for fluids, which states that the product of the cross-sectional area and the velocity of the fluid must remain constant along a streamline. This can be expressed mathematically as:
A1V1=A2V2
Where:
- A1 is the cross-sectional area at the first point,
- V1 is the velocity at the first point,
- A2 is the cross-sectional area at the second point,
- V2 is the velocity at the second point.
1. Convert the Cross-sectional Areas to Square Meters:
- Given A1=4.20cm2 and A2=7.60cm2.
- Convert these areas to square meters:
A1=4.20cm2=4.20×10−4m2
A2=7.60cm2=7.60×10−4m2
2. Identify the Given Values:
- The initial velocity V1=5.18m/s.
3. Use the Continuity Equation to Find V2:
- Rearranging the continuity equation gives:
V2=A1V1A2
- Substitute the known values:
V2=(4.20×10−4m2)(5.18m/s)7.60×10−4m2
4. Calculate V2:
- First, calculate the numerator:
4.20×10−4×5.18=2.1736×10−3m3/s
- Now, divide by A2:
V2=2.1736×10−37.60×10−4≈2.86m/s
5. Final Result:
- The speed of flow at the lower level is approximately V2≈2.86m/s.
- A1 is the cross-sectional area at the first point,
- V1 is the velocity at the first point,
- A2 is the cross-sectional area at the second point,
- V2 is the velocity at the second point.
- Given A1=4.20cm2 and A2=7.60cm2.
- Convert these areas to square meters:
A1=4.20cm2=4.20×10−4m2
A2=7.60cm2=7.60×10−4m2
- The initial velocity V1=5.18m/s.
- Rearranging the continuity equation gives:
V2=A1V1A2
- Substitute the known values:
V2=(4.20×10−4m2)(5.18m/s)7.60×10−4m2
- First, calculate the numerator:
4.20×10−4×5.18=2.1736×10−3m3/s
- Now, divide by A2:
V2=2.1736×10−37.60×10−4≈2.86m/s
- The speed of flow at the lower level is approximately V2≈2.86m/s.
Topper's Solved these Questions
Similar Questions
A horizontal pipeline carries water in a streamline flow. At a point along the pipe, where the cross- sectional area is 10cm2, the water velocity is 1ms−1 and the pressure is 2000 Pa. The pressure of water at another point where the cross-sectional area is 5cm2, is........Pa. (Density of water =103kg.m−3)
View SolutionA horizontal pipeline carries water in a streamline flow. At a point along the pipe, where the cross- sectional area is 10cm2, the water velocity is 1ms−1 and the pressure is 2000 Pa. The pressure of water at another point where the cross-sectional area is 5cm2, is........Pa. (Density of water =103kg.m−3)
View Solution
Knowledge Check
A stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water assuming that it does not rebound? (Density of water =1000kgm−3)
A1.25×103NB2.25×103NC3.25×103ND4.25×103NAn ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
A9:4B3:2C√3:√2D√2:√3An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
A9:4B3:2C√3:√2D√2:√3
A stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall near by what is the force exerted on the wall by the impact of water assuming.that it does not rebound? (Density of water =1000kgm3)
View SolutionA liquid of density ρ is flowing with a speed v through a pipe of cross sectional area A. The pipe is bent in the shape of a right angles as shown. What force should be exerted on the pipe at the corner to keep it fixed?
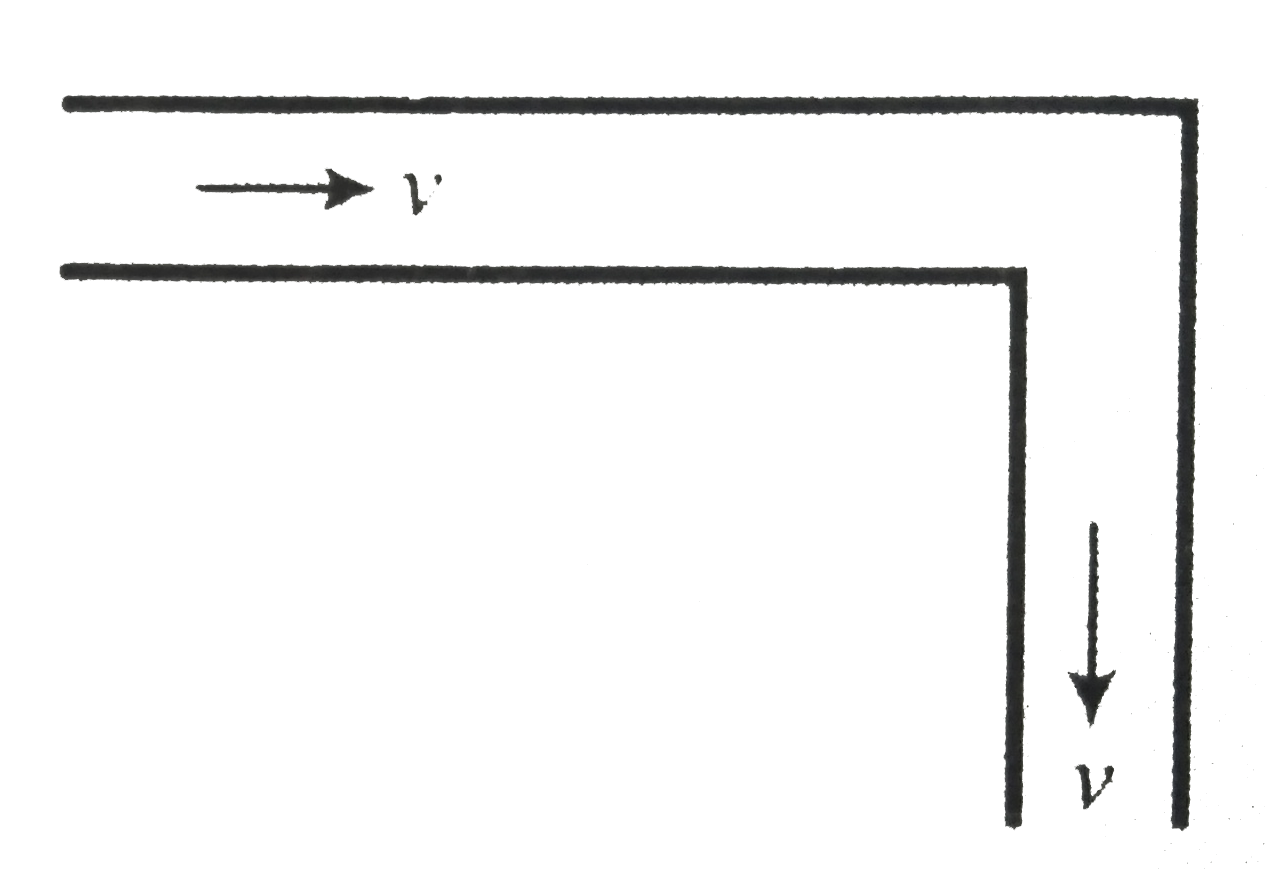
View SolutionAn ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5cm and 3.75cm. The ratio of the velocities in the two pipes is
View SolutionA horizontal pipeline carries water in a streamline flow. At a point along the tube where the cross sectional area is 10−2(m2), the water velcity is 2m/s and the pressure is 8000Pa. The pressure of water at another point where cross sectional area is 0.5×(10)−2(m2) is
View SolutionA stream of water flowing horizontally with a speed of 25ms−1 gushes out of a tube of cross-sectional area 10−3m2, and hits at a vertical wall nearby. What is the force exerted on the wall by the impact of water?
View Solution
