A liquid of density ρ is flowing with a speed v through a pipe of cross sectional area A. The pipe is bent in the shape of a right angles as shown. What force should be exerted on the pipe at the corner to keep it fixed?
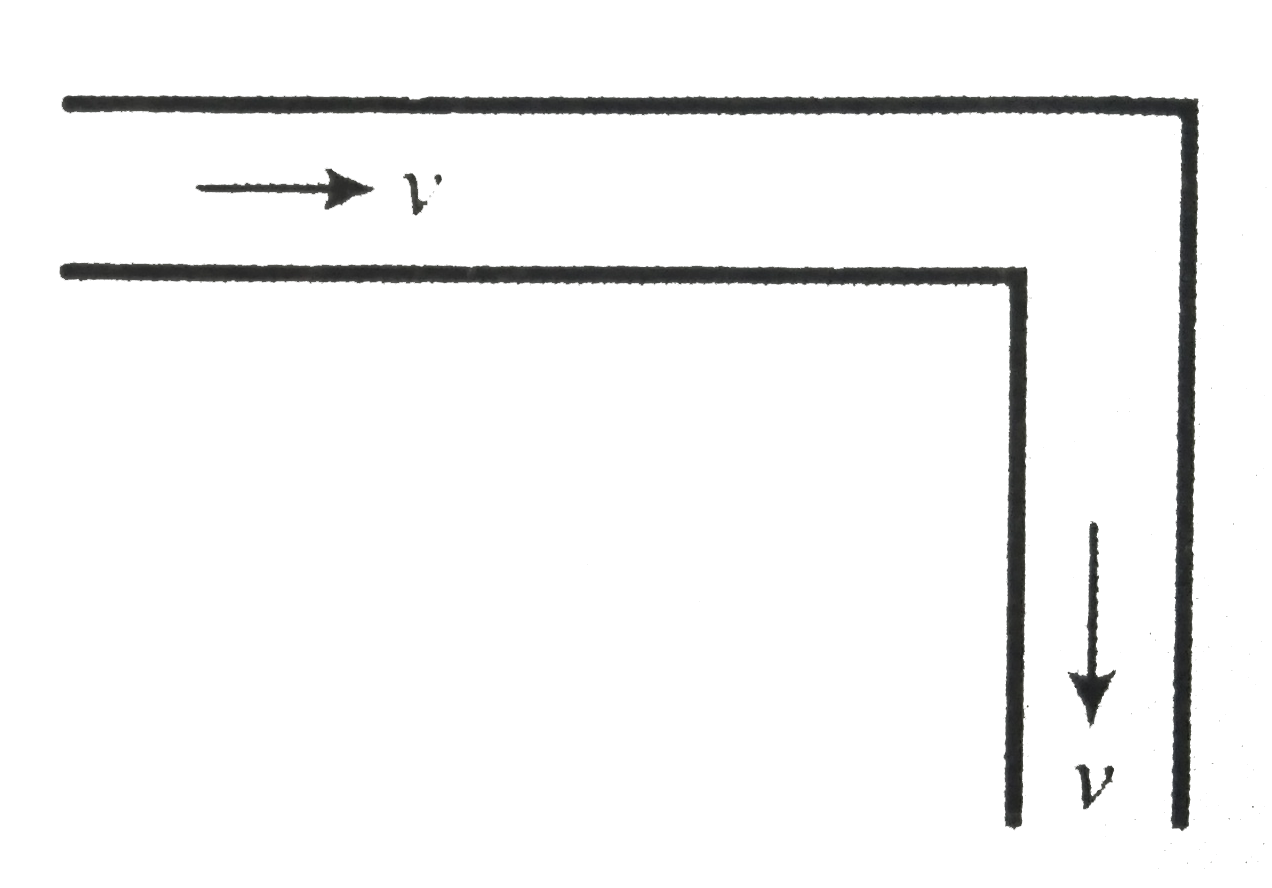
Consider a mass Δm of liquid flowing across the corner in time Δt. We will apply Newton's second law of motion to the mass Δm.
Magnitude of initial momentum
=Pi=(Δm)V
Magnitude of final momentum
=Pf=(Δm)V
Change in momentum =Δ→P=→Pf−→Pi
Δ→P can be calculated by te vector subtraction, geometrically.
As Pi=pf⇒θ=45∘
ΔP=√(P2i+p2f)=√2(Δm)2V2=√2ΔmV
Force exerted on the liquid =ΔPΔt=√2ΔmVΔt=√2VρAV. ltbr> Hence, the pipe must be pushed at the corners as shown in figure. with force F=√2ρAV2 at an angle of 45∘.

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.235videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.319videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
A liquid of density ρ is flowing with a speed V through a pipe of cross sectional area A. What force does the liquid stream exert on wall in x direction if it splashes in the form of a circle after it hits the wall?
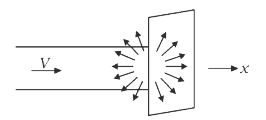 View Solution
View SolutionA pump is used to pump a liquid of density ρ continuously through a pipe of cross, sectional area A. If liquid is flowing with speed v, then average power of pump is
View Solution
Knowledge Check
- Question 1 - Select One
A liquid of density ρ flows along a horizontal pipe of uniform cross-section A with a velocity v through a right angled bend as shown in fig. What force has to be exerted at the bend to hold the pipe in equilibrium ? .
A2aρv2Baρv2/√2C√2aρv2Daρv2
A pump is used to pump a liquid of density ρ continuously through a pipe of cross, sectional area A. If liquid is flowing with speed v, then average power of pump is
View Solution_S01_083_Q01.png)
Water (density ρ) is flowing through the uniform tube of cross-sectional area A with a constant speed v as shown in the figure. Find the magnitude of force exerted by the water on the curved corner of the tube is (neglect viscous forces)View SolutionAn engine pumps a liquid of density 'd' continuously through a pipe of area of cross-section A. If the speed with which the liquid passes through a pipe is v, then force exerted on liquid.
View SolutionA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionAn engine pumps liquid of density ρ continuously through a pipe of cross-section area A. If the speed with which liquid passes through the pipe is v, then the rate at which kinetic energy is being imparted to the liquid by the pump is
View SolutionA liquid is flowing through a pipe of non-uniform cross-section. At a point where area of cross-section of the pipe is less, match the following columns.
 View Solution
View SolutionA pipe of constant cross - section is bent in a horizontal plane as shown in the figure . Points A and B are located on two different streamlines . Then
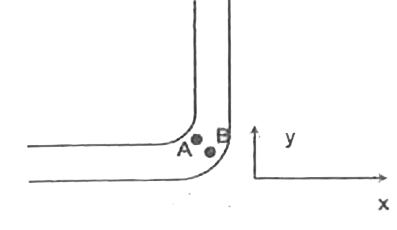 View Solution
View Solution

