Wave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely
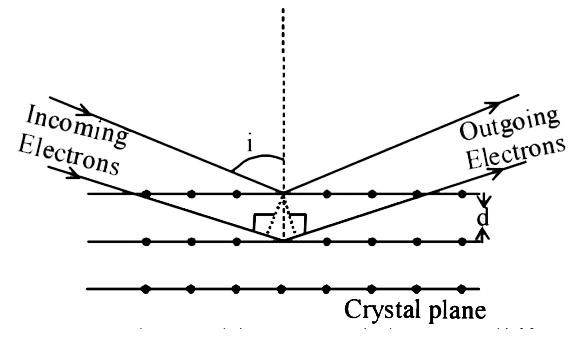
$Wave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see fig) de Brogle wavelength lambda(dB) of electrons can be calculated by the relationship (n is an intenger)$
If a strong diffraction peak is observed when electrons are incident at an angle $i$ from the normal to the crystal planes with distance $d$ between them (see fig) de Brogle wavelength $λ_{d B}$ of electrons can be calculated by the relationship (n is an intenger)

$d cos i = n λ_{d B}$

$d sin i = n λ_{d B}$

$2 d cos i = n λ_{d B}$

$2 d sin i = n λ_{n B}$

Video Solution

Text Solution

Verified by Experts

The Bragg's relation for having an intensity, maximum for diffraction pattern is
$2 d sin θ = n λ$ where $θ$ is glancing angle,
Here, $θ = (90^{\circ} - i)$
$∴ 2 d sin (90^{\circ} - i) = n λ$ or $2 d cos i = n λ$

Class 12 PHYSICS DUAL NATURE OF RADIATION AND MATTER

Topper's Solved these Questions

Knowledge Check

If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see figure), de-Broglie wavelength $λ_{d B}$ of electrons can be calculated by the relationship (n is an integer)
A $d sin i = n λ_{d B}$
B $2 d cos i = n λ_{d B}$
C $2 d sin i = n λ_{d B}$
D $d cos i = n λ_{d B}$
Wave property of electron implies that they will show diffraction effected . Davisson and Germer demonstrated this by diffracting electron from crystals . The law governing the diffraction from a crystals is obtained by requiring that electron waves reflected from the planes of atoms in a crystal inter fere constructiely

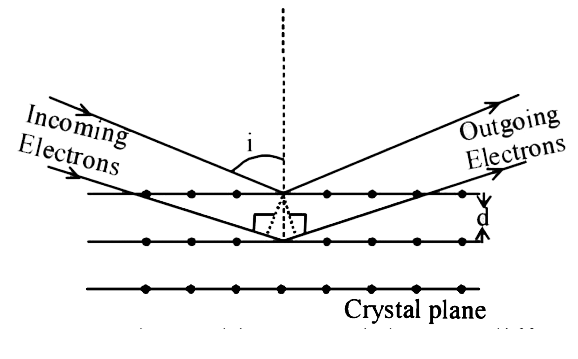
Electron accelerated by potential $V$ are diffracted from a crystal if $d = 1 Å and i = 30^{\circ}, V$ should be about $(h = 6.6 \times 10^{- 34} J s, m_{e} = 9.1 \times 10^{- 31} k g, e = 1.6 \times 10^{- 19} C)$
A $2000 V$
B $50 V$
C $500 V$
D $1000 V$
Wave property of electrons implies that they will show diffraction effects. Davission and Germer demonstrated this by diffracting electrons from crystals. The law governing the diffraction from a crystal is obtained by requiring that electron waves reflected from the planes of atoms in a crystal interfere constructively (see figure)

The surface of a metal is illuminated with the light of $400 n m$ . The kinetic energy of the ejected photoelectrons was found to be $1.68 e V$ . The work function of the metal is : ( $h c = 1240 e V - n m$ )
A $1.51 e V$
B $1.68 e V$
C $3.09 e V$
D $1.42 e V$

PRADEEP-DUAL NATURE OF RADIATION AND MATTER-Exercise

Home
Ask Doubt
Profile

The Bragg's relation for having an intensity, maximum for diffraction pattern is 2dsinθ=nλ where θ is glancing angle, Here, θ=(90∘−i) ∴2dsin(90∘−i)=nλ or 2dcosi=nλ

Topper's Solved these Questions

Similar Questions

Knowledge Check

If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see figure), de-Broglie wavelength λdB of electrons can be calculated by the relationship (n is an integer)

PRADEEP-DUAL NATURE OF RADIATION AND MATTER-Exercise

The Bragg's relation for having an intensity, maximum for diffraction pattern is
$2 d sin θ = n λ$ where $θ$ is glancing angle,
Here, $θ = (90^{\circ} - i)$
$∴ 2 d sin (90^{\circ} - i) = n λ$ or $2 d cos i = n λ$

If a strong diffraction peak is observed when electrons are incident at an angle i from the normal to the crystal planes with distance d between them (see figure), de-Broglie wavelength $λ_{d B}$ of electrons can be calculated by the relationship (n is an integer)