What is the amount of work done in moving a point charge around a circular arc of radius r at the centre of which another point charge is located?
To solve the problem of calculating the work done in moving a point charge around a circular arc of radius r at the center of which another point charge is located, we can follow these steps:
1. Understanding the Setup:
- We have a point charge q located at the center of a circular arc of radius r.
- We want to move another point charge Q along this circular arc.
2. Electric Potential Due to a Point Charge:
- The electric potential V at a distance r from a point charge q is given by the formula:
V=k⋅qr
- Here, k is Coulomb's constant.
3. Potential Along the Circular Arc:
- As we move the charge Q along the circular arc, the distance from the charge q at the center remains constant (equal to r).
- Therefore, the electric potential V at every point along the arc is the same:
V=k⋅qr
4. Work Done in Moving the Charge:
- The work done W in moving a charge Q from one point to another in an electric field is given by:
W=Q⋅(Vf−Vi)
- Here, Vf is the final potential and Vi is the initial potential.
- Since the potential is constant along the circular arc, we have:
Vf=Vi
- Thus, the work done becomes:
W=Q⋅(V−V)=Q⋅0=0
5. Conclusion:
- The amount of work done in moving the point charge Q around the circular arc is zero:
W=0
- We have a point charge q located at the center of a circular arc of radius r.
- We want to move another point charge Q along this circular arc.
- The electric potential V at a distance r from a point charge q is given by the formula:
V=k⋅qr
- Here, k is Coulomb's constant.
- As we move the charge Q along the circular arc, the distance from the charge q at the center remains constant (equal to r).
- Therefore, the electric potential V at every point along the arc is the same:
V=k⋅qr
- The work done W in moving a charge Q from one point to another in an electric field is given by:
W=Q⋅(Vf−Vi)
- Here, Vf is the final potential and Vi is the initial potential.
- Since the potential is constant along the circular arc, we have:
Vf=Vi
- Thus, the work done becomes:
W=Q⋅(V−V)=Q⋅0=0
- The amount of work done in moving the point charge Q around the circular arc is zero:
W=0
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Additional Questions)10videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Fill in the Blanks)11videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Higher Order Thinking Skills & Advanced Level (QUESTIONS WITH ANSWERS)10videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
On rotating a point charge g around a charge Q in a circle of radius r, the work done is
Aq.2πrBq.2πOrCzeroDQ2ε0r - Question 2 - Select One
The work done in carrying a charge q once around a circle of radius r with a charge Q placed at the centre centre will be
AQq4πε0r2BQq4πε0rCzeroDQq24πε0r - Question 3 - Select One
The work done in carrying a charge q once around a circle of radius r with a charge Q placed at the centre centre will be
AQq4πε0r2BQq4πε0rCzeroDQq24πε0r
There is a ball of radius r having uniformly distributed volume charge Q on it and there is a spherical shell of radius r having uniformly distributed surface charge Q on it. The two spheres are far apart. (a) A point charge q is moved slowly from the centre of the shell (through a small hole in it.) to the centre of the ball. Find work done by the external agent in the process. (b) The two spheres are brought closer so that their centers are separated by 4r. Now calculate the amount of work needed in slowly moving a point charge q from the centre of the shell to the centre of the ball. Assume that charge on one ball does not alter the charge distribution of the other. Does your answers in (a) and (b) differ? Why?
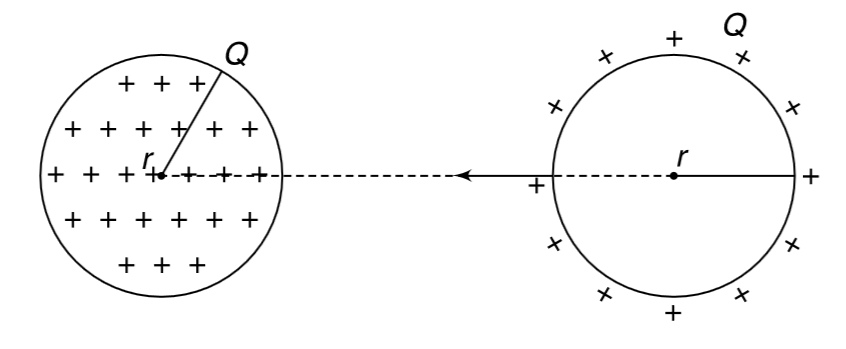 View Solution
View SolutionThe work done in carrying a point charge form one point to another in an electrostatic field depends on the path along which the point charge is carried.
View SolutionCalculate the amount of work done in moving a 1μC charge from one point to another if potential difference between both the points is 12V.
View SolutionThe work done in carrying a charge Q1 once round a circle of radius R with a charge Q2 at the centre is
View SolutionThe amount of work done in moving a charge of 5 C across two points having a potential difference of 15 Volts is equal to
View Solution

