What is the angle between P and Q the cross product of (P+Q)and(P−Q)?
90∘
tan−1(p/Q)
tan−1(Q/p)
0∘
The correct Answer is:A
To find the angle between the vectors P and Q in the context of the cross product of (P+Q) and (P−Q), we can follow these steps:
1. Understand the Cross Product:
The cross product of two vectors A and B is given by:
A×B=|A||B|sin(θ)^n
where θ is the angle between the vectors A and B, and ^n is the unit vector perpendicular to the plane formed by A and B.
2. Identify the Vectors:
We need to compute the cross product (P+Q)×(P−Q).
3. Use the Distributive Property of Cross Product:
The cross product can be expanded as follows:
(P+Q)×(P−Q)=P×P+P×(−Q)+Q×P+Q×(−Q)
Since the cross product of any vector with itself is zero, we have:
P×P=0andQ×Q=0
Thus, the expression simplifies to:
(P+Q)×(P−Q)=0−P×Q+Q×P
4. Recognize the Anti-Symmetry of the Cross Product:
The cross product is anti-symmetric, meaning:
Q×P=−(P×Q)
Therefore, we can rewrite the expression as:
(P+Q)×(P−Q)=−P×Q−P×Q=−2(P×Q)
5. Determine the Angle:
The result −2(P×Q) indicates that the direction of the resultant vector is perpendicular to both P and Q. Since the cross product results in a vector that is perpendicular to the plane formed by P and Q, the angle between P and Q must be 90∘.
Final Answer:
The angle between the vectors P and Q is 90∘.
The cross product of two vectors A and B is given by:
A×B=|A||B|sin(θ)^n
where θ is the angle between the vectors A and B, and ^n is the unit vector perpendicular to the plane formed by A and B.
We need to compute the cross product (P+Q)×(P−Q).
The cross product can be expanded as follows:
(P+Q)×(P−Q)=P×P+P×(−Q)+Q×P+Q×(−Q)
Since the cross product of any vector with itself is zero, we have:
P×P=0andQ×Q=0
Thus, the expression simplifies to:
(P+Q)×(P−Q)=0−P×Q+Q×P
The cross product is anti-symmetric, meaning:
Q×P=−(P×Q)
Therefore, we can rewrite the expression as:
(P+Q)×(P−Q)=−P×Q−P×Q=−2(P×Q)
The result −2(P×Q) indicates that the direction of the resultant vector is perpendicular to both P and Q. Since the cross product results in a vector that is perpendicular to the plane formed by P and Q, the angle between P and Q must be 90∘.
The angle between the vectors P and Q is 90∘.
Topper's Solved these Questions
Similar Questions
What is the angle between →P and the resultant of (→P+→Q) and (→P−→Q) ?
View SolutionThe angles between P+Q and P-Q will be
View Solution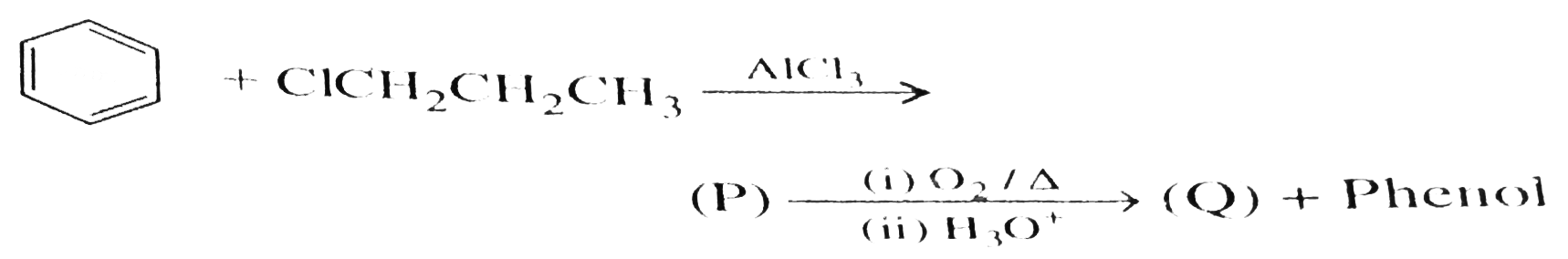
The majore products (P) and (Q) are:
View SolutionWhat is the angle between (→P+→Q) and (→P×→Q)?
View SolutionWhat can be the angle between (→P+→Q) and (→P−→Q) ?
View SolutionThree forces P, Q and R are acting on a particel in the plane, the angle between P and Q and that between Q and R are 150∘ and 120∘ respectively. Then for equilibrium, forces P, Q and R are in the ratio
View SolutionThree forces P, Q and R are acting on a particel in the plane, the angle between P and Q and that between Q and R are 150∘ and 120∘ respectively. Then for equilibrium, forces P, Q and R are in the ratio
View SolutionThe product of the sines of the angles of a triangle is p and the product of their cosines is q. Show that the tangents of the angles are the roots of the equation qx3−px2+(1+q)x−p=0.
View SolutionGiven that P=Q=R. If →P+→Q=→R then the angle between →P and →R is θ1. If →P+→Q+→R=→0 then the angle between →P and →R is θ2. The relation between θ1 and θ2 is :-
View SolutionThe resultant →Pand→Q is perpendicular to →P. What is the angle between →Pand→Q?
View Solution
