Three forces P, Q and R are acting on a particel in the plane, the angle between P and Q and that between Q and R are and respectively. Then for equilibrium, forces P, Q and R are in the ratio
The correct Answer is:D
To solve the problem of finding the ratio of forces P, Q, and R acting on a particle in equilibrium, we can follow these steps:
Step 1: Understand the Angles
We are given:
- The angle between forces P and Q is 150∘.
- The angle between forces Q and R is 120∘.
Step 2: Set Up the Coordinate System
Assume that force P is acting along the positive x-axis. Therefore:
- Force P can be represented as P=P^i.
- The angle between P and Q is 150∘, so we can represent Q in terms of its components:
Qx=Qcos(150∘)=−Qcos(30∘)=−Q⋅√32
Qy=Qsin(150∘)=Qsin(30∘)=Q⋅12
Step 3: Represent Force R
The angle between Q and R is 120∘. Since Q is at 150∘ from P, R will be at:
Angle of R from P=150∘+120∘=270∘
Thus, R acts downward along the negative y-axis:
Rx=0
Ry=−R
Step 4: Apply Equilibrium Conditions
For the system to be in equilibrium, the sum of the forces in both the x and y directions must equal zero.
In the x-direction:
P+Qx+Rx=0
Substituting the values:
P−Q⋅√32+0=0⇒P=Q⋅√32
In the y-direction:
Qy+Ry=0
Substituting the values:
Q⋅12−R=0⇒R=Q⋅12
Step 5: Find the Ratios
Now we have:
1. P=Q⋅√32
2. R=Q⋅12
To find the ratio P:Q:R:
P:Q:R=(√32Q):Q:(12Q)
Dividing through by Q:
P:Q:R=√32:1:12
Step 6: Simplify the Ratio
To eliminate the fractions, multiply through by 2:
P:Q:R=√3:2:1
Final Answer
Thus, the ratio of forces P, Q, and R for equilibrium is:
√3:2:1
We are given:
- The angle between forces P and Q is 150∘.
- The angle between forces Q and R is 120∘.
Assume that force P is acting along the positive x-axis. Therefore:
- Force P can be represented as P=P^i.
- The angle between P and Q is 150∘, so we can represent Q in terms of its components:
Qx=Qcos(150∘)=−Qcos(30∘)=−Q⋅√32
Qy=Qsin(150∘)=Qsin(30∘)=Q⋅12
The angle between Q and R is 120∘. Since Q is at 150∘ from P, R will be at:
Angle of R from P=150∘+120∘=270∘
Thus, R acts downward along the negative y-axis:
Rx=0
Ry=−R
For the system to be in equilibrium, the sum of the forces in both the x and y directions must equal zero.
P+Qx+Rx=0
Substituting the values:
P−Q⋅√32+0=0⇒P=Q⋅√32
Qy+Ry=0
Substituting the values:
Q⋅12−R=0⇒R=Q⋅12
Now we have:
1. P=Q⋅√32
2. R=Q⋅12
P:Q:R=(√32Q):Q:(12Q)
Dividing through by Q:
P:Q:R=√32:1:12
To eliminate the fractions, multiply through by 2:
P:Q:R=√3:2:1
Thus, the ratio of forces P, Q, and R for equilibrium is:
√3:2:1
Similar Questions
The angles between P+Q and P-Q will be
View SolutionGiven that P 12, Q = 5 and R = 13 also P+Q=R, then the angle between P and Q will be
View SolutionIf P+Q=Rand|P|=|Q|=√3and|R|==3, then the angle between P and Q is
View SolutionIf vector P,QandR have magnitude 5,12,and 13 units and →P+→Q=→R, the angle between Q and R is
View Solution−10μC,40μC and q are the charges on three identical conductors P,Q and R respectively, Now P and Q attract each other with a force F when they are separated by a distance d. Now P and Q are made in contact with each other and then separated . Again Q and R are touched and they are separated by a distance 'd' . The repulsive force between Q and R is 4F . Then the charge q is:
View SolutionThree particales P,Q and R are placedd as per given Masses of P,Q and R are √3m√3m and m respectively The gravitational force on a fourth particle 'S' of mass m is equal to
 .
.
View Solution∠PQR=100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR
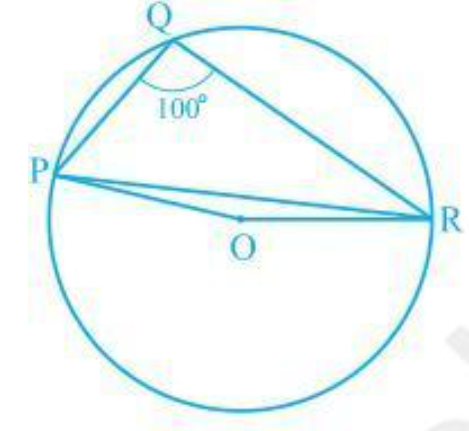
View SolutionConsider three charged bodies P,Q and R. If P and Q repel each other and P attracts R, what is the nature of force between Q and R ?
View SolutionIf P,Q and R are three collinear points such that →PQ=→a and →QR = →b. Find the vector →PR .
View SolutionIf the resultannt of two forces of magnitudes P and Q acting at a point at an angle of 60∘ is √7Q, then P/Q is
View Solution
