What is the displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward half a revolution? Take the radius of the wheel as R and the x-axis as the forward direction?
From figure, during half revolution of the wheel, the point A covers AC=π horizontal distance, and BC = 2R vertical distance.

x=πRandy=2R. Displacement,
s=√x2+y2=√(πR)2+(2R)2=R√π2+4
and θ=Tan−1(yx)=Tan−1(2RπR)=Tan−1(2π) with x-axis.
i.e Displacement has magnitude R√π2+4 and makes an angle Tan−1(2i) with x-axis.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Vectors & Scalars)
25 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Addition & Subtractions of Vectors)
10 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
What is the displacement of the point of a wheel initially in contact with the ground when the wheel rolls forward half a revolution ? Take the radius of the wheel as R and the the x - axis as the forward direction ?
View SolutionA Wheel of circumference C is at rest on the ground.When the wheel rolls forward through half a revolution ,then the displacement of point contact will be
View SolutionA wheel of perimeter 4π is rolling on a horizontal surface. The displacement of the point of contact of wheel and ground when the wheel completes one quarter of revolution is
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
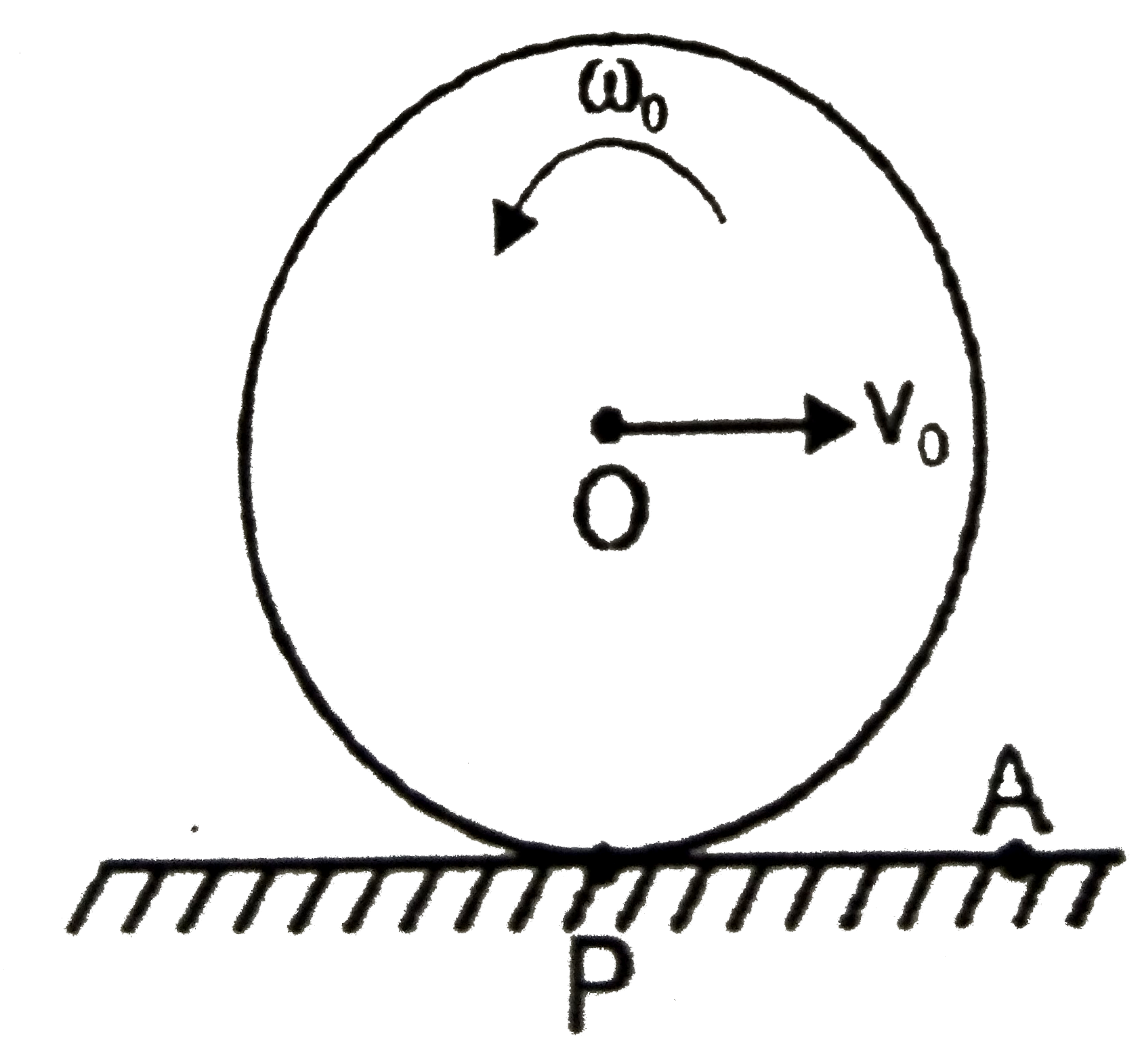
If the wheel comes to permanent rest after sometimes, then :
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
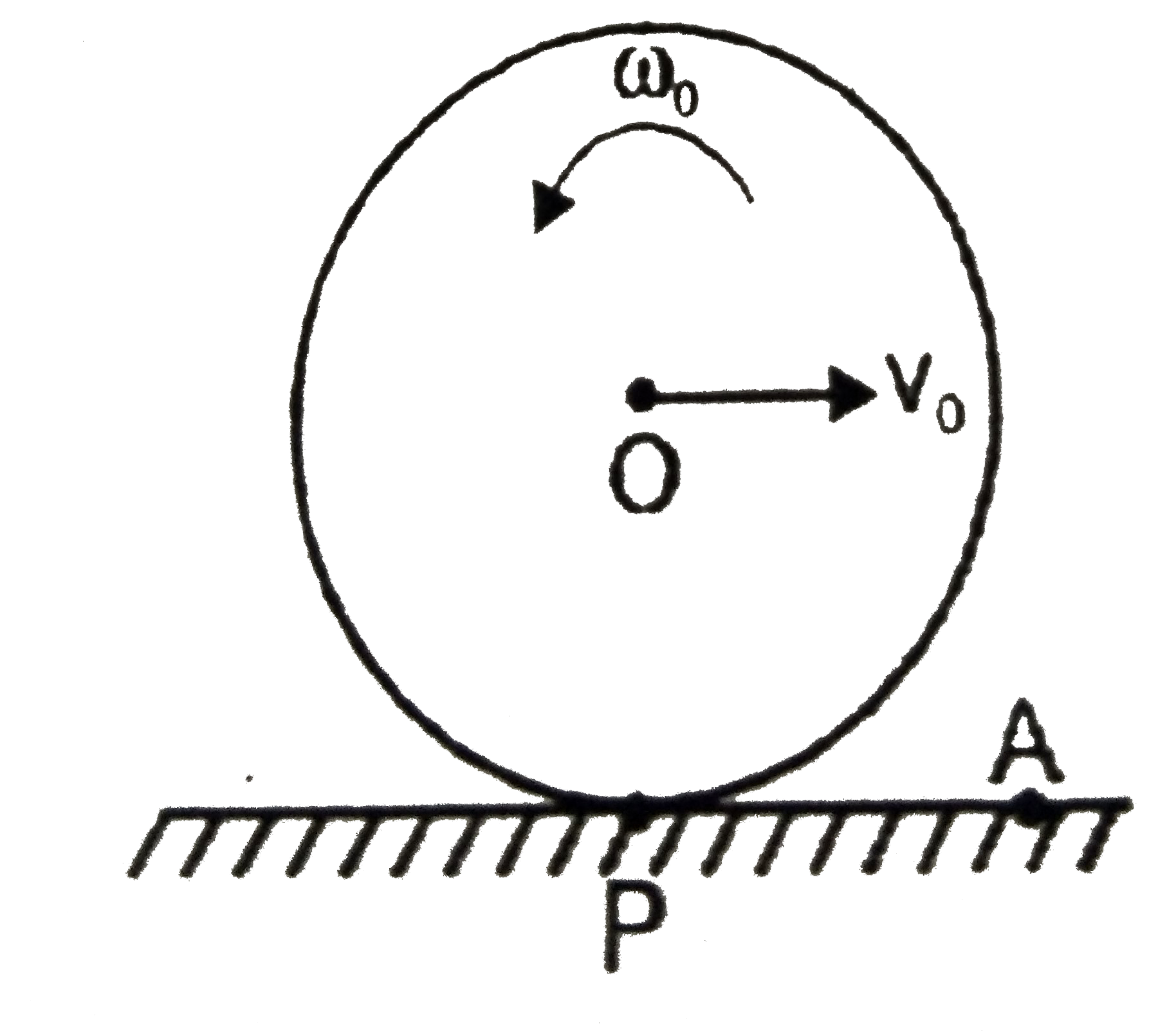
If above question , distance travelled by centre of mass of the wheel before it stops is −
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
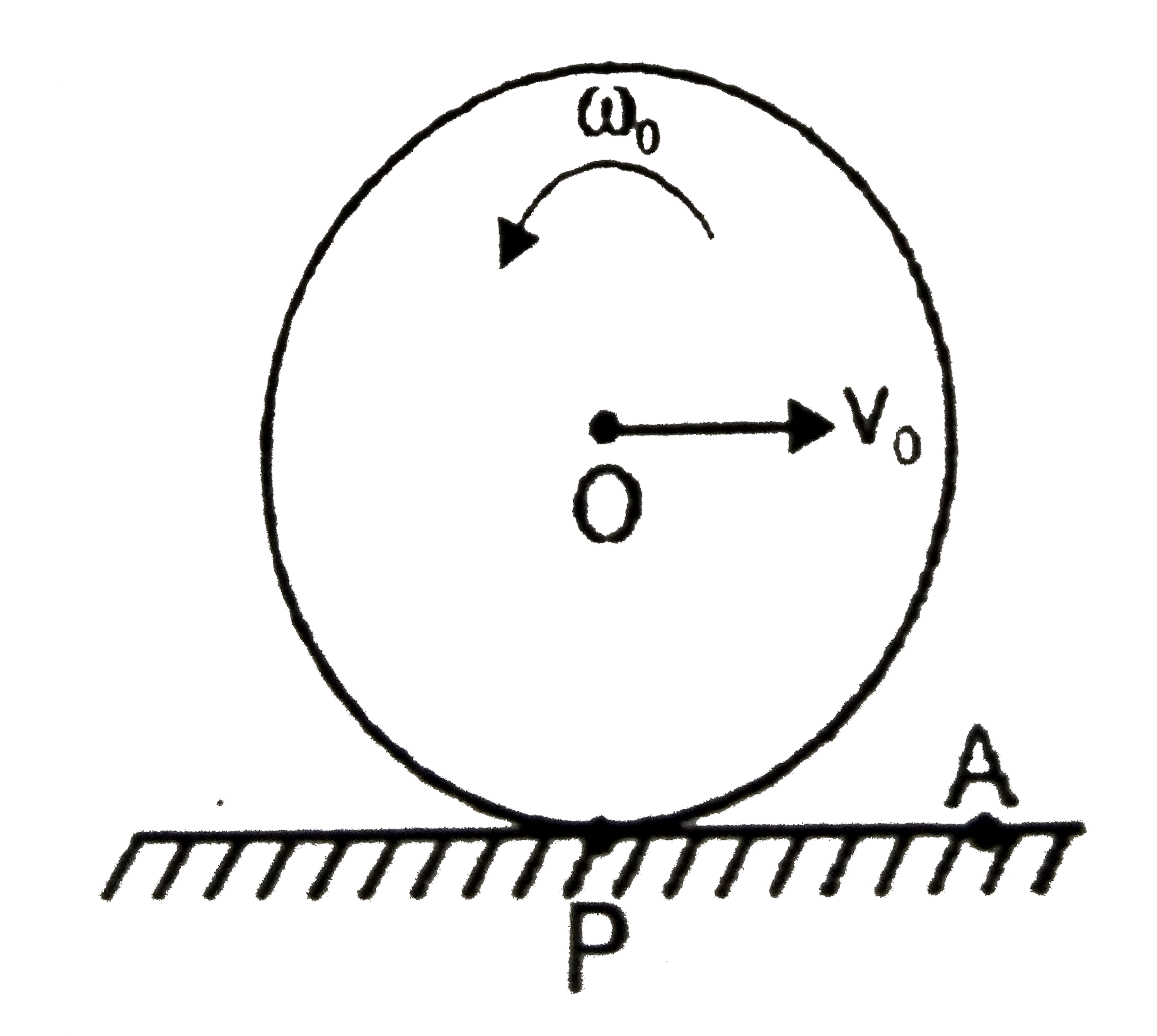
Which of the following is conserved ?
View SolutionIf a given point P is in contact with ground initially and wheel of radius R is in pure rolling, then the displacement of point P when point P reaches topmost of the sphere for the first time will be

View SolutionA bicycle wheel rolls without slipping on a horizonatal floor.W hich one of the following is true about the motion of points on the rim of the wheel, relative to the axis at the wheel's centre?

View SolutionThe drwing shows a bicycle wheel of radius r, resting against a small step whose height is h=r/5. A clockwise torque increases, there comes a time when the wheel just begins to rise up and loses contact with the ground. Let this torque be T. What is the magniitude of the horizontal component of the acceleration of the centre of the wheel when a torque of 2T is applied? Assume that the wheel doesn't slip at the edge of the step when this torque is applied (ignore the mass of the spokes).

View SolutionA constant horizontal force of 10N is applied at the centre of a wheel of mass 10kg and radius 0.30m. The wheel rolls without slipping on the horizontal surface, and the acceleration of the centre of mass is 0.60m/s2.
a. What are the magnitude and direction of the frictional force on the wheel?
b. What is the rotational inertia of the wheel about an axis through its centre of mass and perpendicular to the plane of the wheel?
View Solution
