What is the flux through two opposite faces of the cube when a charge q0 is placed at the centre of the cube?
q0ε0
0
q03ε0
q06ε0
To find the electric flux through two opposite faces of a cube when a charge q0 is placed at the center, we can use Gauss's law. Here's the step-by-step solution:
Step 1: Understand Gauss's Law
Gauss's law states that the total electric flux Φ through a closed surface is equal to the charge enclosed q divided by the permittivity of free space ϵ0:
Φ=qϵ0
Step 2: Calculate the Total Flux Through the Cube
Since the charge q0 is placed at the center of the cube, the total electric flux through the entire surface of the cube can be calculated as:
Φtotal=q0ϵ0
Step 3: Determine the Flux Through One Face
The cube has six faces, and by symmetry, the flux will be uniformly distributed across all faces. Therefore, the flux through each face of the cube is:
Φface=Φtotal6=q06ϵ0
Step 4: Calculate the Flux Through Two Opposite Faces
Since we are interested in the flux through two opposite faces, we can simply multiply the flux through one face by 2:
Φtwo faces=2×Φface=2×q06ϵ0=2q06ϵ0=q03ϵ0
Final Answer
The total electric flux through two opposite faces of the cube is:
Φtwo faces=q03ϵ0
Gauss's law states that the total electric flux Φ through a closed surface is equal to the charge enclosed q divided by the permittivity of free space ϵ0:
Φ=qϵ0
Since the charge q0 is placed at the center of the cube, the total electric flux through the entire surface of the cube can be calculated as:
Φtotal=q0ϵ0
The cube has six faces, and by symmetry, the flux will be uniformly distributed across all faces. Therefore, the flux through each face of the cube is:
Φface=Φtotal6=q06ϵ0
Since we are interested in the flux through two opposite faces, we can simply multiply the flux through one face by 2:
Φtwo faces=2×Φface=2×q06ϵ0=2q06ϵ0=q03ϵ0
The total electric flux through two opposite faces of the cube is:
Φtwo faces=q03ϵ0
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 EXERCISE - SECTION - B22videos
SAMPLE PAPER 9
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 EXERCISE - SECTION - C3videos
SAMPLE PAPER 9
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION-C6videos
SAMPLE PAPER 7
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER SELF- ASSESSMENT -(10)EXERCISE - SECTION-B17videos
SAMPLE PAPER SELF- ASSESSMENT -(10)
Similar Questions
The total flux through the faces of the cube with side of length a if a charge q is placed at corner A of the cube is
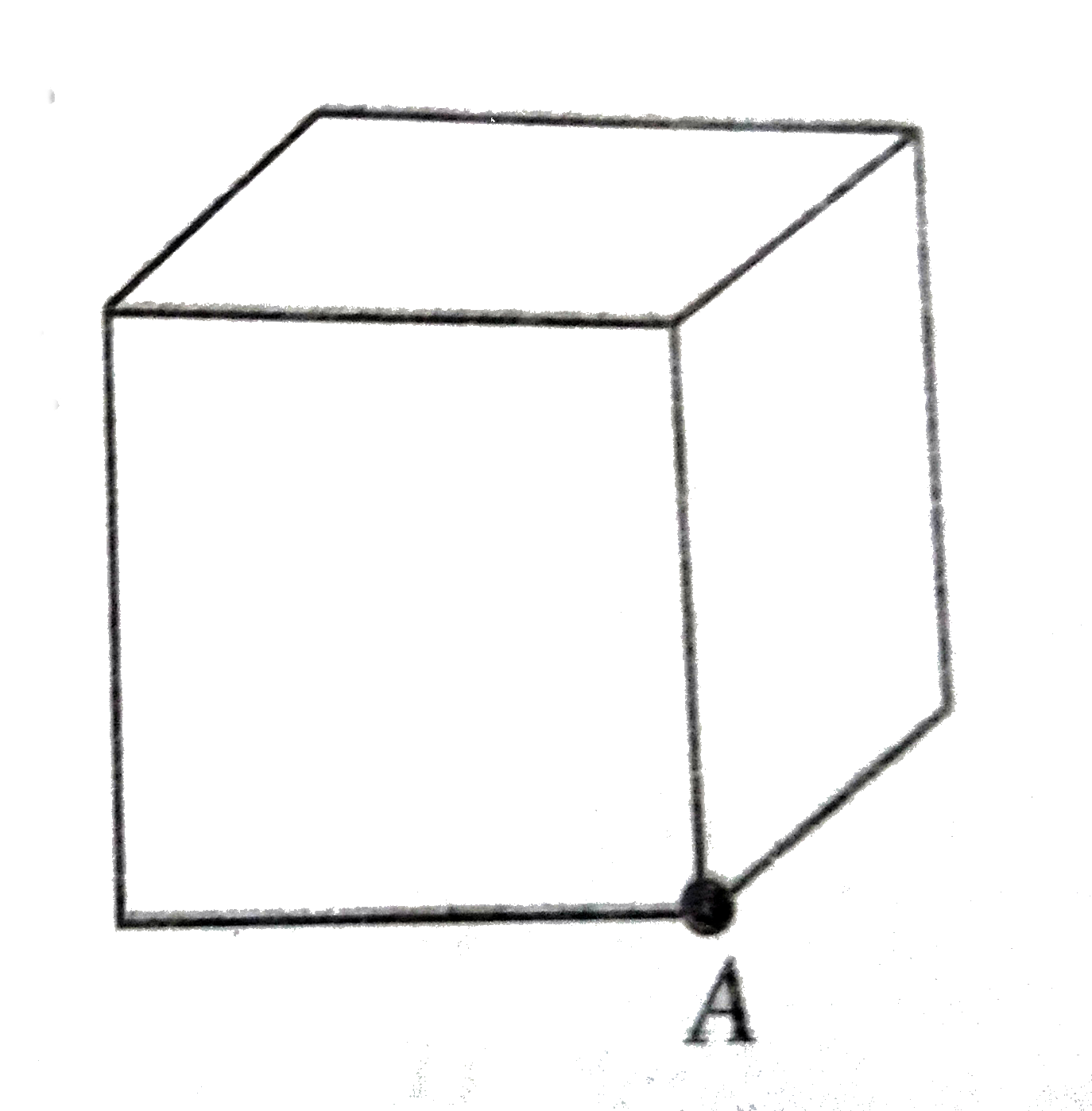 View Solution
View SolutionWhat will be the total flux throguh the faces of the cube, Fig with side of length a if a charge q is placed at (a) A : a corner of the cube (b) B : mid-point of an edge of the cube (c ) C : center of a face of the cube (d) D : mid-point of B and C.
View Solution
Knowledge Check
- Question 1 - Select One
The total electric flux through a cube when a charge 8q is placed at one corner of the cube is
Aε0qBε0qCqε0Dq4πε0 - Question 2 - Select One
The total electric flux through a cube when a charge 8q is placed at one comer of the cube is
Aε0qBε0qC4πε0qDqε0 - Question 3 - Select One
What is electric flux assoacited with one of faces of the cube, when a charge (q) is enclosed in a cube ?
A6qε0B3qε0Cq3ε0Dq6ε0
The total flux through the faces of the cube with side of length a ,if a charge q is placed at B (mid-point of an edge of the cube), is ϕ, and if a charge q is placed at C (centre of a face of the cube), is ϕ2. Find ϕ2ϕ1.
'(##CEN_KSR_PHY_JEE_C18_E01_018_Q06##)'View SolutionThe total flux through the faces of the cube with side of length a if a charge q is placed at corner A of the cube is
 View Solution
View SolutionTwelve charges have been placed at the centre of each side of a cube as shown in the figure. Find the magnitude of Electric force acting on a charge Q placed at the centre of the cube. Take the side length of the cube to be r.
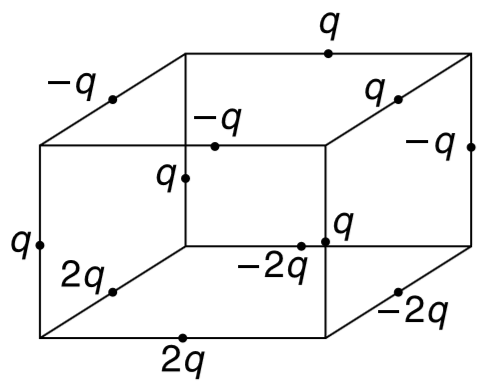 View Solution
View SolutionWhat is the flux link through a cube of side l if a charge 2q is placed at one end of cube ?
View SolutionIf 8 identical charges of -g each are placed at the eight corners of a cube of side b, then electrostatic potential energy of a charge +q0 placed at the centre of the cube will be
View Solution

