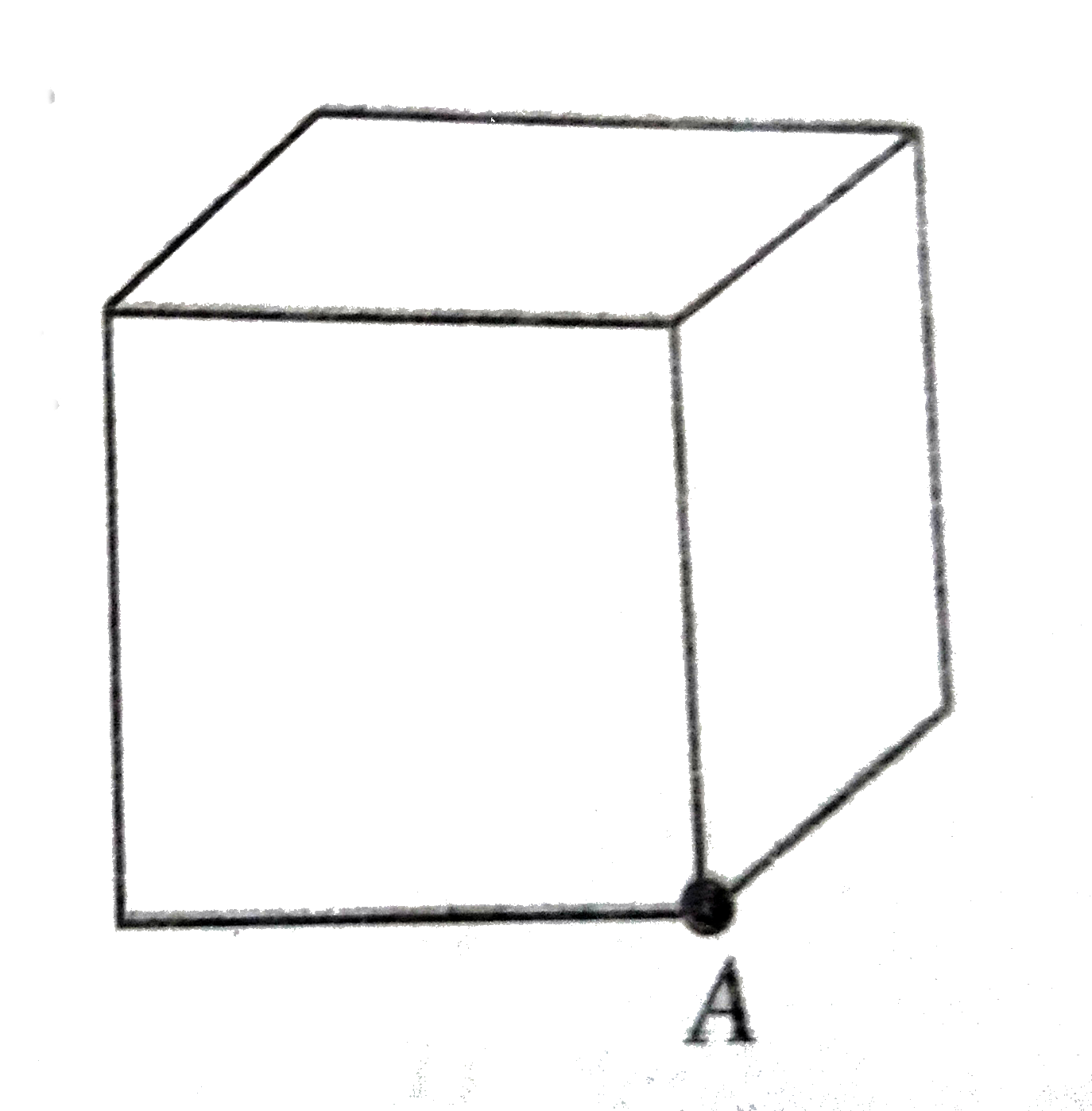
What is the flux link through a cube of side l if a charge 2q is placed at one end of cube ?
qε0
q8ε0
2qε0
q4ε0
The correct Answer is:D
To solve the problem of finding the electric flux through a cube of side l when a charge 2q is placed at one end of the cube, we can follow these steps:
1. Understand Gauss's Law:
Gauss's Law states that the total electric flux Φ through a closed surface is equal to the charge Q enclosed by that surface divided by the permittivity of free space ϵ0:
Φ=Qϵ0
2. Identify the Charge and Geometry:
In this case, we have a charge 2q placed at one end of the cube. Since the charge is not enclosed within the cube, we need to consider how much of the total flux from this charge actually passes through the cube.
3. Determine the Total Flux from the Charge:
The total electric flux produced by the charge 2q can be calculated using Gauss's Law:
Φtotal=2qϵ0
4. Calculate the Fraction of Flux through the Cube:
Since the charge 2q is located at one corner of the cube, we can visualize that the total flux emanating from the charge is distributed equally among the eight surrounding cubes (since a charge at a corner of a cube is shared by eight cubes). Therefore, the flux through the cube is:
Φcube=Φtotal8=2q8ϵ0=q4ϵ0
5. Final Result:
Thus, the electric flux through the cube is:
Φ=q4ϵ0
Conclusion:
The electric flux through the cube when a charge 2q is placed at one end of the cube is q4ϵ0.
Gauss's Law states that the total electric flux Φ through a closed surface is equal to the charge Q enclosed by that surface divided by the permittivity of free space ϵ0:
Φ=Qϵ0
In this case, we have a charge 2q placed at one end of the cube. Since the charge is not enclosed within the cube, we need to consider how much of the total flux from this charge actually passes through the cube.
The total electric flux produced by the charge 2q can be calculated using Gauss's Law:
Φtotal=2qϵ0
Since the charge 2q is located at one corner of the cube, we can visualize that the total flux emanating from the charge is distributed equally among the eight surrounding cubes (since a charge at a corner of a cube is shared by eight cubes). Therefore, the flux through the cube is:
Φcube=Φtotal8=2q8ϵ0=q4ϵ0
Thus, the electric flux through the cube is:
Φ=q4ϵ0
The electric flux through the cube when a charge 2q is placed at one end of the cube is q4ϵ0.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - PHYSICS WALLAHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - NEET PAST 5 YEARS QUESTIONS
7 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - PHYSICS WALLAHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - NEET PAST 5 YEARS QUESTIONS
7 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PHYSICS WALLAHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Neet past 5 years questions
16 Videos
- ELECTROMAGNETIC INDUCTION BOOK - PHYSICS WALLAHCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - NEET PAST 5 YEARS QUESTIONS
10 Videos
Similar Questions
Knowledge Check
What is the flux through a cube of side 'a' if a point charge of q is at one of its corner :
A2q∈0Bq8∈0Cq∈0D2q2∈06a2What is the flux through a cube of side 'a' if a point charge of q is at one of its corner :
A2q∈0Bq8∈0Cq∈0D2q2∈06a2What is the flux through a cube of side 'a' if a point charge of q is at one of its corner?
Aq2ε0B2qε0CQ8ε0Dqε0
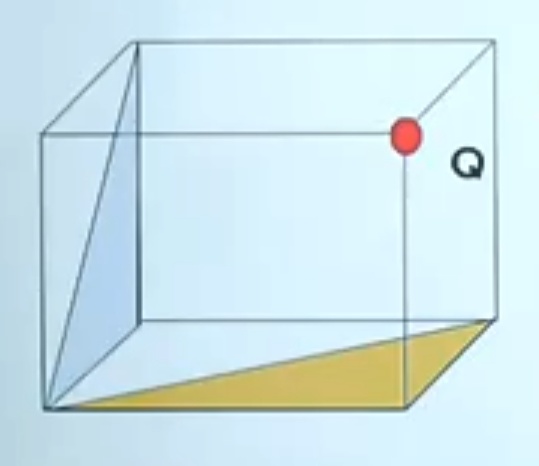
Find the flux through shaded region, due to charge Q placed at vertex of a cube
View SolutionWhat will be the total flux throguh the faces of the cube, Fig with side of length a if a charge q is placed at (a) A : a corner of the cube (b) B : mid-point of an edge of the cube (c ) C : center of a face of the cube (d) D : mid-point of B and C.
View SolutionThe total electric flux through a cube when a charge 8q is placed at one comer of the cube is
View SolutionThe total electric flux through a cube when a charge 8q is placed at one corner of the cube is
View SolutionElectric flux through a cube with charge q inside is
View Solution