What is the mass of the planet that has a satellite whose time period is and orbital radius is ?
The correct Answer is:B
Suppose that a satellite of mass describes a circular orbit around a planetof mass .
This force must be mass times the cenripetal acceleration.
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
According to Kepler's law of planetary motion, if T represents time period and r is orbital radius, then for two planets these are related as
View SolutionThe period of revolution of a satellite depends upon the radius of the orbit, the mass of the planet and the gravitational constant. Prove that the square of the period varies as the cube of the radius.
View Solution
Knowledge Check
Match the Column I with Column II
For a satellite in circular orbit
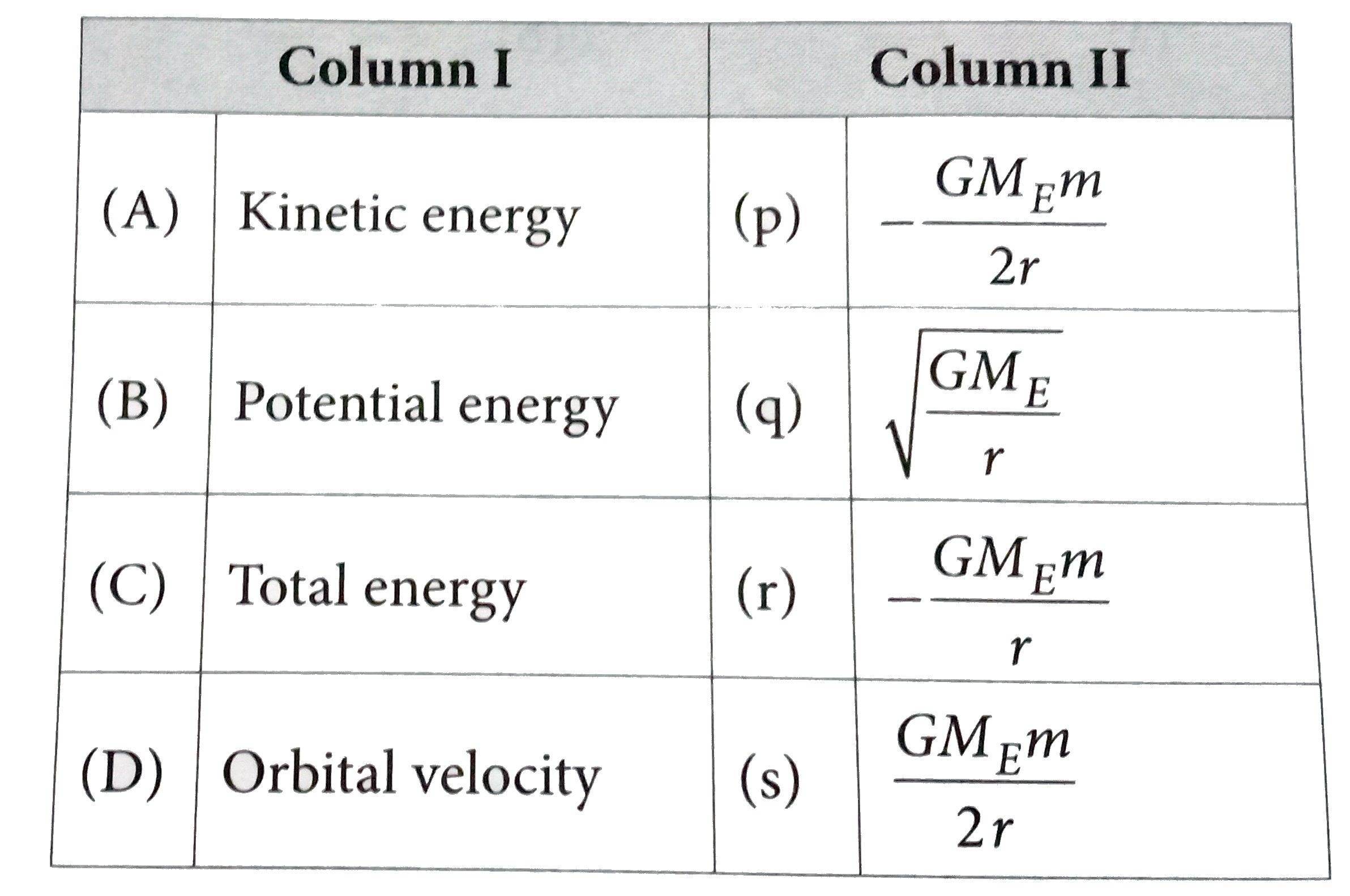
(where ME is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )AA-r, B-s,C-q,D-pBA-q,B-p,C-r,D-sCA-p,B-q,C-s,D-rDA-s,B-r,C-p,D-qA satellite is orbiting the earth in a circular orbit of radius r. Its
AKnetic enegy varies as rBangular momentum varies as 1√rClinear momentum varies as 1rDfrequency of revolution varies as 1r3/2The time period T of the moon of planet mars (mass Mm) is related to its orbital radius R as (G=gravitational constant)
AT2=4π2R3GMmBT2=4π2GR3MmCT2=4πR3GMmDT2=4πMmGR3
A satellite of mass 1000kg is rotating around the earth in a circular orbit of radius 3R. What extra energy should be given to this satellite if it is to be lifted into an orbit of radius 4R?
View SolutionThe radius of orbit of a planet is two times that of the earth. The time period of planet is
View SolutionThe radius of a planet is R1 and a satellite revolves round it in a circle of radius R2. The time period of revolution is T. find the acceleration due to the gravitation of the plane at its surface.
View SolutionAn artificial satellite (mass m) of a planet (mass M) revolves in a circular orbit whose radius is n times the radius R of the planet in the process of motion the satellite experiences a slight resistance due to cosmic dust. Assuming the force of resistance on satellite to depend on velocity as F=av2 where 'a' is a constant caculate how long the satellite will stay in the space before it falls on to the planet's surface.
View SolutionThe time period of earth is taken as T and its distance from sun as R. What will be the distance of a certain planet from sun whose time period is 64 times that of earth ?
View Solution
