What is the moment of inertia of a
(i) uniform circular ring of mass 2 kg about its 4 m diameter ?
(ii) a thin disc about an axis coinciding with a diameter ?
Video Solution
Text Solution
The moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to it is given by, I=MR2
According to the theorem of perpendicular axis, Iz,Ix+Iy
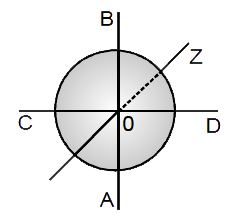
Now x and y-axes are along the diameter of the disc nad by symmetry
Ix=Iy⇒Iz=2Ix⇒Ix=MR2
The moment of inertia of ring about of its diameter
Ix=MR22=(2)(2)22=4kg-m2
(ii) Similarly, moment of inertia about the diameter of disc
I=12(12MR2)=14MR2.
|
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Knowledge Check
Moment of inertia of a uniform circular ring of mass 2kg and diameter 1m about its diameter is
A0.25kgm2B0.5kgm2C1kgm2D2kgm2The moment of inertia of a uniform circular disc of mass M and of radius R about one of its diameter is
A14MR2B12MR2C23MR2D25MR2The moment of inertia of a thin circular disc of mass M and radius R about any diameter is
AMR24BMR22CMR2D2MR2
Calculate the moment of inertia of uniform circular disc of mass 500 g, radius 10 cm about : diameter of the disc
View SolutionCalculate moment of inertia of a uniform circular ring of mass 1.5kg and diameter 50cm about a diameter of the ring.
View SolutionFind the moment of inertia of uniform ring of mass M and radius R about a diameter.
View SolutionCalculate the moment of inertia of
a. a ring of mass M and radius R about an axis coinciding with the diameter of the ring.
b. as thin disc about an axis coinciding with the diameter.
View SolutionThe moment of inertia of a thin circular disc of mass M and radius R about any diameter is
View Solution
