Find the moment of inertia of uniform ring of mass M and radius R about a diameter.
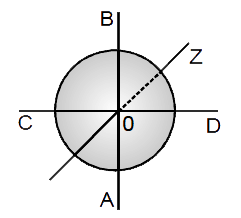
Let AB and CD be two mutually perpendicular diameters of the ring. Take them ax X and Y-axes and the line perpendicular to the plane of the ring through the centre as the Z-axis. The moment of inertia of the ring about the Z-axis is I=MR2. As the ring is uniform, all of its diameter equivalent and so Ix=I+y, From perpendicular axes theorem,
Iz=Ix+Iy' Hence Ix=Iz2=MR22
Similarly, the moment of inertia of a uniform disc about a diameter is MR2/4
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 190videos
ROTATIONAL MOTION
- BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 240videos
ROTATIONAL MOTION
- BOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-438videos
RAY OPTICS
- BOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 334videos
SEMI CONDUCTOR AND LOGIC GATES
Similar Questions
Knowledge Check
- Question 1 - Select One
Moment of inertia of a disc of mass 'M' and radius 'R' about the diameter is
AMR22BMR24CMR23DMR212 - Question 2 - Select One
Moment of inertia of a circular wire of mass M and radius R about its diameter is :
AMR22BMR2C2MR2DMR24 - Question 3 - Select One
Moment of inertia of a circular wire of mass M and radius R about its diameter is
AMR22BMR2C2MR2DMR24
Moment of inertia of a uniform circular ring of mass M and radius R about a diameter of ring is………………. .
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be
 View Solution
View Solution(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5,whereM is the mass of the sphere and R is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be 14MR2, find the moment of inertia about an axis normal to the disc passing through a point on its edge.View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be :-
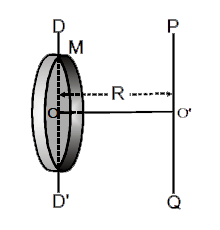 View Solution
View SolutionFind the moment of inertia of a half uniform ring (mass m, radius r) about its center.
View Solution

