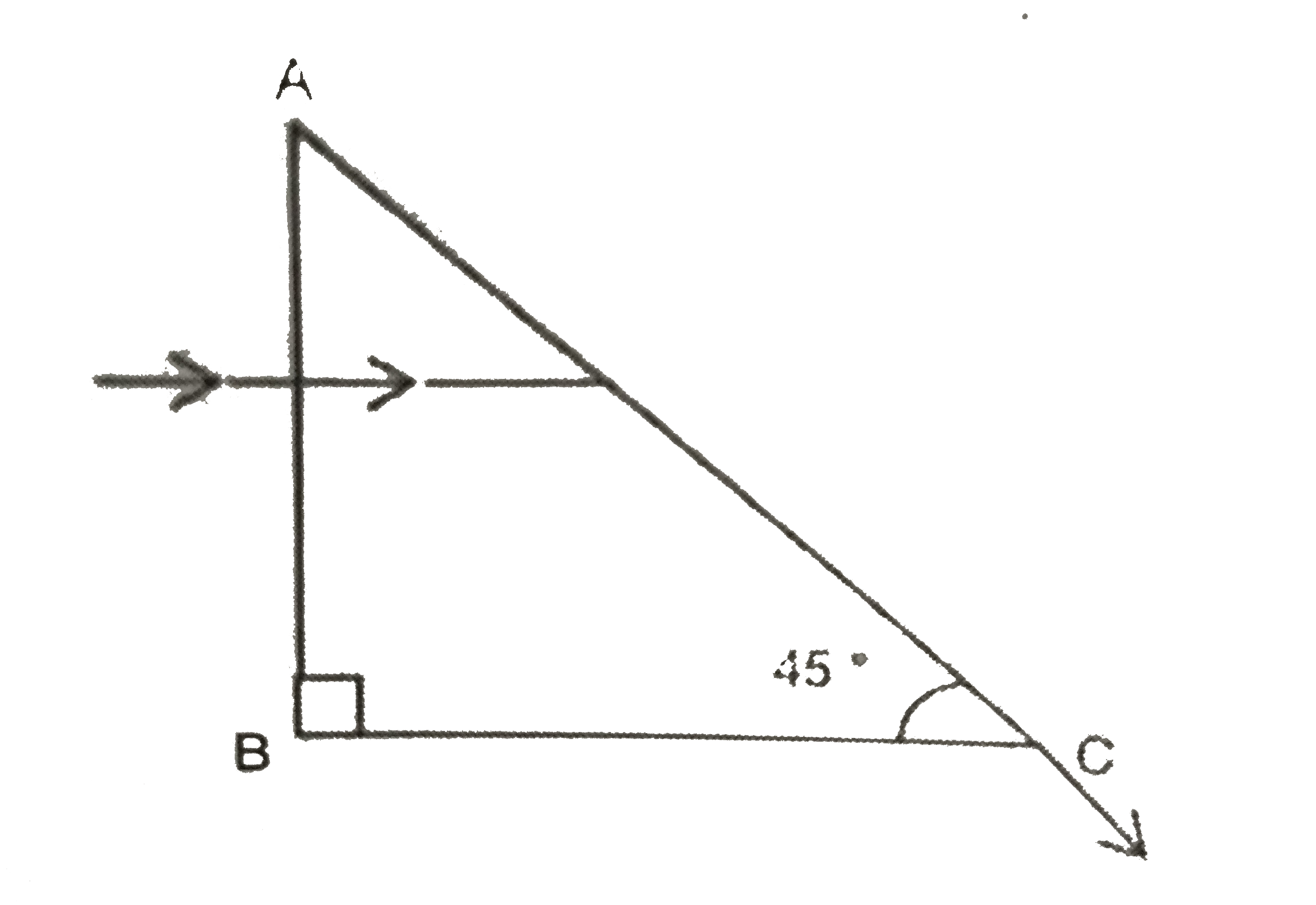
What is the required condition, if the light incident on one face, does not emerge from the other face ?

Text Solution

Verified by Experts

For no emergence, $r_{2} > θ_{c}$
$A - r_{1} > θ_{c}$
$\sin (A - r_{1}) > {\sin θ}_{c}$
$\sin A {\cos r}_{1} - \cos A {\sin r}_{1} > \frac{1}{μ}$
$\sin A [{\cos r}_{1}] - \cos A [\frac{\sin i}{μ}] > \frac{1}{μ}$
$\Rightarrow μ \sin A \sqrt{1 - \sin^{2} r_{1}} - \cos A \sin i > 1$
$\Rightarrow μ \sin A \sqrt{(1 - \frac{\sin^{2} i}{μ^{2}})} > 1 + \cos A \sin i$
$\Rightarrow \sin A \cdot \sqrt{μ^{2} - \sin^{2}} i > (1 + \cos A \sin i)$
Squaring both sides,
$\sin^{2} A (μ^{2} - \sin^{2} i) > {(1 + \cos A \sin i)}^{2}$
$μ^{2} \sin^{2} A - \sin^{2} A \sin^{2} i > 1 + \cos^{2} A \sin^{2} i + 2 \cos A \sin i$
$μ^{2} \sin^{2} A > 1 + (\cos^{2} A + \sin^{2} A) \sin^{2} i + 2 \cos A \sin i$
$μ^{2} \sin^{2} A > 1 + \sin^{2} i + 2 \cos A \sin i$
The greatest value of sin $i = 1$
$\Rightarrow μ^{2} \sin^{2} A > 1 + 1 + 2 \cos A$
$μ^{2} (2^{2} \sin^{2} . \frac{A}{2} \cos^{2} . \frac{A}{2}) > 2 (1 + \cos A)$
$4 μ^{2} \sin^{2} . \frac{A}{2} \cos^{2} . \frac{A}{2} > 4 \cos^{2} . \frac{A}{2} \Rightarrow μ^{2} > \frac{1}{\sin^{2} . \frac{A}{2}}$
$μ > \cos e c (\frac{A}{2})$ .

Updated on:21/07/2023

What is the required condition, if the light incident on one face of a prism, does not emerge from the other face?
A $n < cosec (\frac{A}{2})$
B $n < sec (\frac{A}{2})$
C $n > sec A$
D $n > cosec (\frac{A}{2})$
For an equilateral prism, it is observed that when a ray strikes grazingly at one face, it emerges grazingly at the other face, its refractive index will be
A $\frac{\sqrt{3}}{2}$
B $\frac{2}{\sqrt{3}}$
C2
D $\frac{4}{3}$