A ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.

ng=1.6
At the first face,
Angle of incidence I0=0
angle of refraction r1=0
At the second face,
Angle of incidence r2=C=?
Angle of refraction i2=90∘
We have for critical incidence at the second face
n=1sinC⇒sinC=1n=11.6=0.6250
C=38∘41.
We have A=r1+r=0+C=38∘41.
Topper's Solved these Questions
- REFRACTION OF LIGHT BOOK - CENGAGE PHYSICSCHAPTER - REFRACTION OF LIGHT EXERCISE - OLYMPIAD AND NSE LEVEL EXCERCISES
10 Videos
- REFRACTION OF LIGHT BOOK - CENGAGE PHYSICSCHAPTER - REFRACTION OF LIGHT EXERCISE - GENERAL EXERCISE
32 Videos
- OPTICAL INSTRUMENTS BOOK - CENGAGE PHYSICSCHAPTER - OPTICAL INSTRUMENTS EXERCISE - OLYMPLAD AND NTSE LEVEL EXERCISES
10 Videos
- SOURCES OF ELECTRIC CURRENTBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF ELECTRIC CURRENTEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
Similar Questions
If a light ray incidents normally on one of the faces of the prism of refractive index 2 and the emergent ray just grazes the second face of the prism, then the angle of deviation is
View SolutionIf a light ray incidents normally on one of the faces of the prism of refractive index 2 and the emergent ray just grazes the second face of the prism, then the angle of deviation is
View Solution
Knowledge Check
If a light ray incidents normally on one of the faces of the prism of refractive index 2 and the emergent ray just grazes the second face of the prism, then the angle of deviation is
A0∘B30∘C45∘D60∘A ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
A7.5∘B5∘C15∘D2.5∘A ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
A7.5∘B5∘C15∘D2.5∘
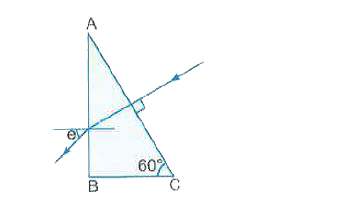
Calculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index √3. How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air ?
View SolutionA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
View SolutionA ray of light incident at an angle θ on a refracting face of a prism emerges from the other face normally. If the angle of the prism is 5∘ and the prism is made of a material of refractive index 1.5, the angle of incidence is.
View SolutionLight falls at normal incidence on one face of a glass prism of refractive index √2. Then the angle of emergence when the angle of the prism is 45∘
View SolutionA ray of light is incident normally on one of the equal faces of a right isosceles prism of refractive index 1.5. The angle between incident and emergent rays is
View Solution
