What will be the ratio of time of flights of two projectiles fired at angles of θand90∘−θ ?
To find the ratio of the time of flight of two projectiles fired at angles θ and 90∘−θ, we can follow these steps:
Step 1: Understand the formula for time of flight
The time of flight T for a projectile is given by the formula:
T=2usinθg
where u is the initial velocity, g is the acceleration due to gravity, and θ is the angle of projection.
Step 2: Write the time of flight for both angles
1. For the first projectile fired at angle θ:
T1=2usinθg
2. For the second projectile fired at angle 90∘−θ:
T2=2usin(90∘−θ)g
Step 3: Simplify sin(90∘−θ)
Using the trigonometric identity:
sin(90∘−θ)=cosθ
we can rewrite the time of flight for the second projectile:
T2=2ucosθg
Step 4: Find the ratio of the time of flights
Now, we can find the ratio of the time of flights T1 and T2:
T1T2=2usinθg2ucosθg=sinθcosθ=tanθ
Final Answer
Thus, the ratio of the time of flights of the two projectiles is:
T1T2=tanθ
---
The time of flight T for a projectile is given by the formula:
T=2usinθg
where u is the initial velocity, g is the acceleration due to gravity, and θ is the angle of projection.
1. For the first projectile fired at angle θ:
T1=2usinθg
T2=2usin(90∘−θ)g
Using the trigonometric identity:
sin(90∘−θ)=cosθ
we can rewrite the time of flight for the second projectile:
T2=2ucosθg
Now, we can find the ratio of the time of flights T1 and T2:
T1T2=2usinθg2ucosθg=sinθcosθ=tanθ
Thus, the ratio of the time of flights of the two projectiles is:
T1T2=tanθ
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Revision Exercises (Additional Questions)
4 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Revision Exercises (Fill in the Blanks)
9 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Higher Order Thinking Skills & Advanced Level
6 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
Knowledge Check
The time of flight of the projectile is:
Aa√2bgBa√bgC√2abgD√a2bgGalileo writes that for angles of projection of a projectile at angles (45+θ) and (45−θ), the horizontal ranges described by the projectile are in the ratio of (if θ≤45)
A2:1B1:2C1:1D2:3In Rutherford scattering experiment, wha will be the ratio of impact parameter for scattering angles θ1=90∘andθ2=120∘
A1B√2C2D√3
Ratio between maximum range and square of time of flight in projectile motion is
View SolutionA projectile is fired at an angle θ with horizontal. (a) Show that its trajectory is a parabola (b) Prove that for a given velocity of projection the horizontal range is same for (90∘−θ) (c) Obtain an expression for velocity of projectile at any instant.
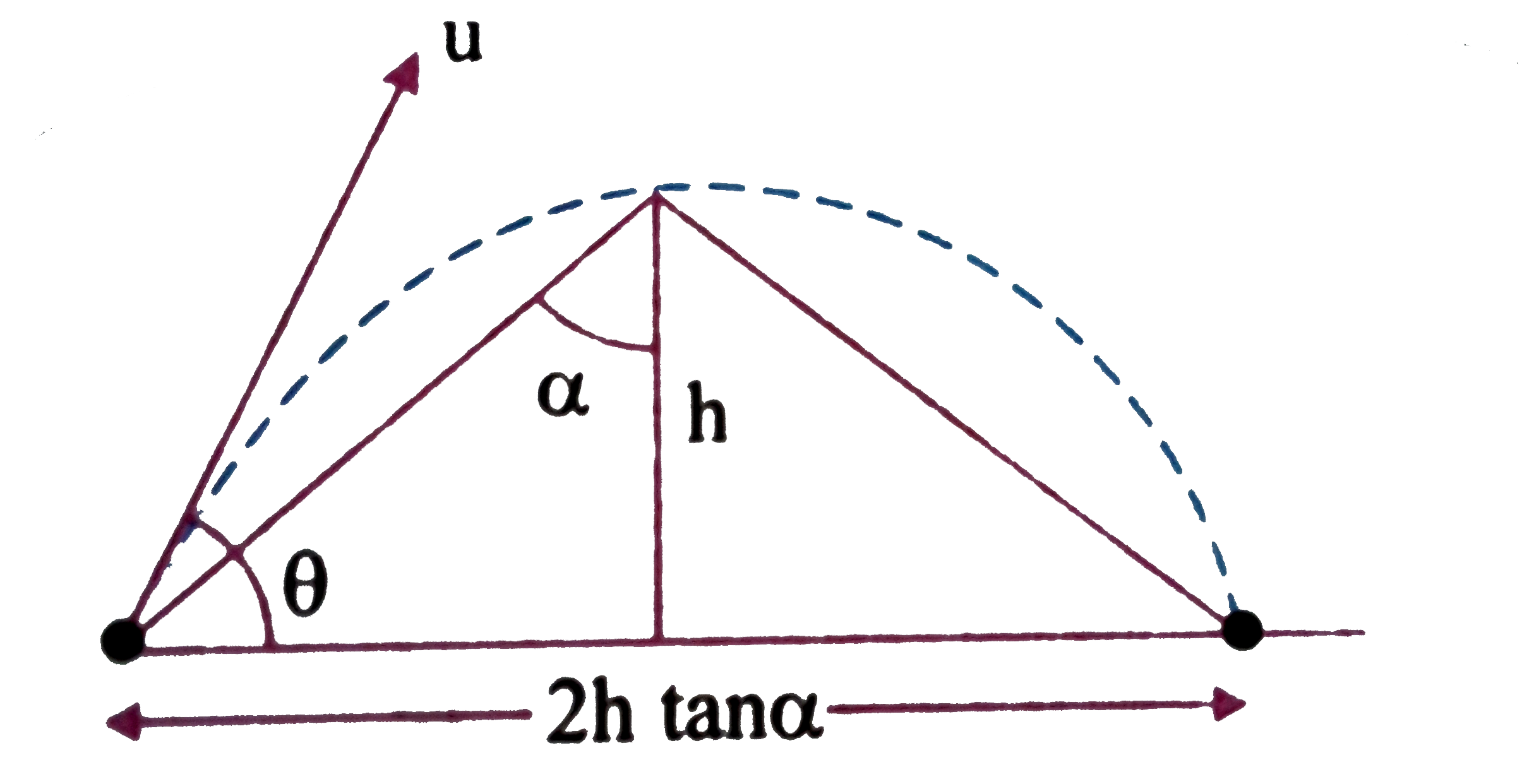
View SolutionA projectile is fired from the base of coneshaped hill. The projectile grazes the vertex and strikes the hill again at the base.If α be the half-angle of the cone, h its height, u the initial velocity of projection and θ angle of projection, then then θtanθis
View SolutionOn an inclined plane two particles AandB are projected with same speed at the same angle with the horizontal, particle A down and particle B up the plane. If the ratio of time of flight of AandB is cotθ, where θ is the angle at which B is projected measured from inclined plane, find the angle at which particles are projected.
View SolutionA projectile has a time of flight T and range R. If the time of flight is doubled, keeping the angle of projection same, what happens to the range ?
View Solution
