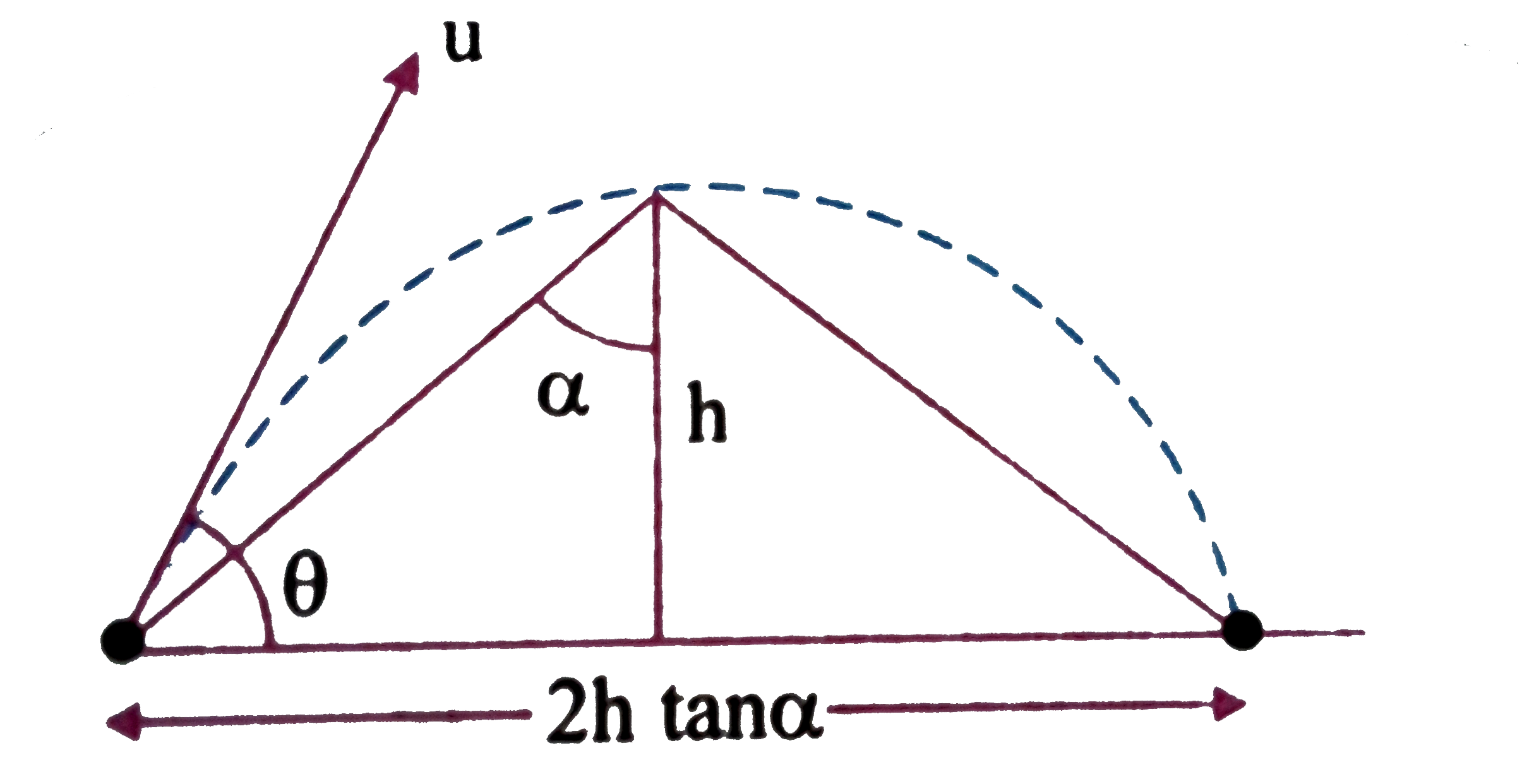
A projectile is fired from the base of coneshaped hill. The projectile grazes the vertex and strikes the hill again at the base.If α be the half-angle of the cone, h its height, u the initial velocity of projection and θ angle of projection, then then θtanθis
The correct Answer is:B
Here range =2htanα=u2sin2θg and h=u2sin2θ2g Dividing 2tanα=2sin2θsin2θ⇒tanα=2cotθ
∴u22ghsin2θ=2gh(2cotα√1+4cot2α)=2gh(1+4cot2α)4cot2α=gh(12tan2α+2)
tanθ=2cotα
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-Vi single answer30videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-Vi multiple answer16videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Passage15videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
Similar Questions
A projectile is fired from the base of cone shaped hill. The projectle grazes the vertex and strikes the hill again at the base. If α be the half-angle of the cone, h its height, u the initial velocity of projection and θ angle of projection, then tanθtanα is:
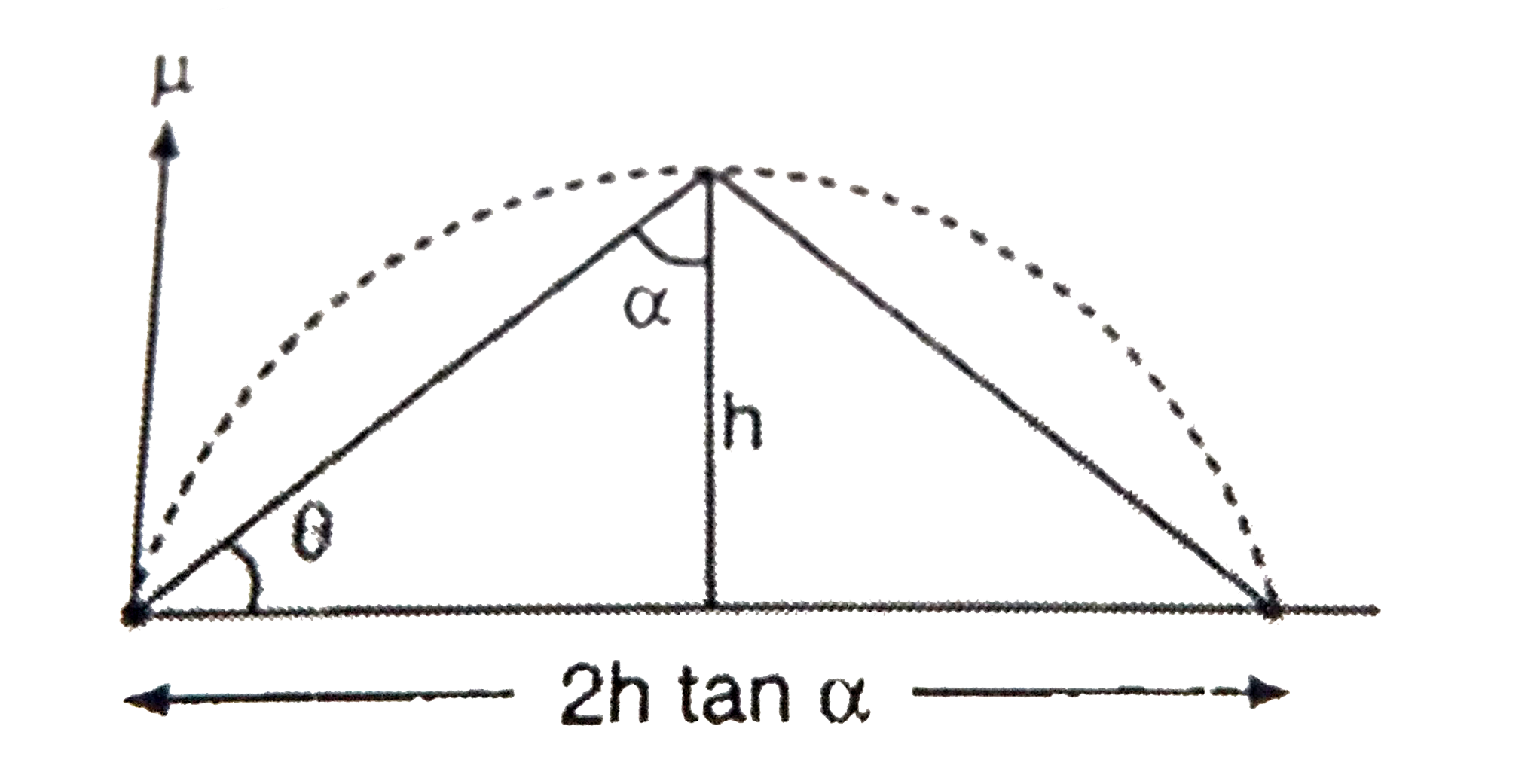 View Solution
View SolutionA particle is projected over a traingle from one end of a horizontal base and grazing the vertex falls on the other end of the base. If α and β be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ.
View Solution
Knowledge Check
- Question 1 - Select One
If a projectile having horizontal range of 24 acquires a maximum height of 8, then its initial velocity and the angle of projection are
A5√g,sin−1(0.6)B5√g,sin−1(0.8)C24√g,sin−1(0.6)D8√g,sin−1(0.8) - Question 2 - Select One
A projectile fired with initial velocity u at some angle θ has a range R . If the initial velocity be doubled at the same angle of projection, then the range will be
A2RBR/2CRD4R - Question 3 - Select One
A particle is thrown over a triangle from one end of horizontal base and grazing over the vertex falls on the other end of the base. If α,β are the base angles and θ the angle of projection, then
Atanθ=tanα−tanβBtanθ=tanβ−tanαCtanθ=tanα+tanβDNone of these
A particle is projected over a triangle from one extremity of its horizontal base. Grazing over the vertex, it falls on the other extremity of the base. If aandb are the base angles of the triangle and θ the angle of projection, prove that tanθ=tan∝+tanβ.
View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .
View SolutionThe speed of a projectile at its maximum height is half of its initial speed. The angle of projection is .
View SolutionA particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If 30∘and60∘ be the base angles and θ the angle of projection then tanθ is
View SolutionThe velocity at the maximum height of a projectile is half of its velocity of projection u. Its range on the horizontal plane is
View Solution

