When a body of density and volume V is floating in a liquid of density
its true weight is
loss in its weight is
its apparent weight is zero
its density is greater than that of liquid .
The correct Answer is:C
To solve the problem of a body of density d1 and volume V floating in a liquid of density d2, we need to analyze the concepts of true weight, loss in weight, and apparent weight. Here’s a step-by-step breakdown of the solution:
Step 1: Understand True Weight
The true weight of an object is given by the formula:
True Weight=mass×g
Where mass can be calculated as:
mass=density×volume=d1×V
Thus, the true weight W can be expressed as:
W=d1×V×g
Step 2: Calculate Loss in Weight
When the object is submerged in a liquid, it experiences an upward buoyant force. The buoyant force Fb is given by Archimedes' principle:
Fb=density of liquid×volume of object×g=d2×V×g
The loss in weight of the object when submerged in the liquid is equal to the buoyant force:
Loss in Weight=Fb=d2×V×g
Step 3: Determine Apparent Weight
The apparent weight of the object when it is floating in the liquid is given by:
Apparent Weight=True Weight−Loss in Weight
Substituting the expressions we derived:
Apparent Weight=(d1×V×g)−(d2×V×g)
This simplifies to:
Apparent Weight=V×g×(d1−d2)
Step 4: Analyze Conditions for Floating
For an object to float, the density of the object d1 must be less than the density of the liquid d2:
d1<d2
If d1<d2, then d1−d2<0, which means the apparent weight will be less than the true weight but not zero.
Conclusion
From the analysis:
1. The true weight is d1×V×g.
2. The loss in weight is d2×V×g.
3. The apparent weight is V×g×(d1−d2), which is not zero as long as d1 is less than d2.
Final Answer
The correct option is:
- Loss in weight is V×d2×g.
The true weight of an object is given by the formula:
True Weight=mass×g
Where mass can be calculated as:
mass=density×volume=d1×V
Thus, the true weight W can be expressed as:
W=d1×V×g
When the object is submerged in a liquid, it experiences an upward buoyant force. The buoyant force Fb is given by Archimedes' principle:
Fb=density of liquid×volume of object×g=d2×V×g
The loss in weight of the object when submerged in the liquid is equal to the buoyant force:
Loss in Weight=Fb=d2×V×g
The apparent weight of the object when it is floating in the liquid is given by:
Apparent Weight=True Weight−Loss in Weight
Substituting the expressions we derived:
Apparent Weight=(d1×V×g)−(d2×V×g)
This simplifies to:
Apparent Weight=V×g×(d1−d2)
For an object to float, the density of the object d1 must be less than the density of the liquid d2:
d1<d2
If d1<d2, then d1−d2<0, which means the apparent weight will be less than the true weight but not zero.
From the analysis:
1. The true weight is d1×V×g.
2. The loss in weight is d2×V×g.
3. The apparent weight is V×g×(d1−d2), which is not zero as long as d1 is less than d2.
The correct option is:
- Loss in weight is V×d2×g.
Topper's Solved these Questions
- THRUST AND PRESSUREBOOK - MTG IIT JEE FOUNDATIONCHAPTER - THRUST AND PRESSUREEXERCISE - Exercise (Match the following)
5 Videos
- THRUST AND PRESSUREBOOK - MTG IIT JEE FOUNDATIONCHAPTER - THRUST AND PRESSUREEXERCISE - Exercise (Assertion & Reason type)
10 Videos
- THRUST AND PRESSUREBOOK - MTG IIT JEE FOUNDATIONCHAPTER - THRUST AND PRESSUREEXERCISE - NCERT Section
10 Videos
- SOUNDBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SOUNDEXERCISE - Olympiad/HOTS Corner
15 Videos
- WORK AND ENERGYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - WORK AND ENERGYEXERCISE - Olympaid/HOTS Corner
20 Videos
Similar Questions
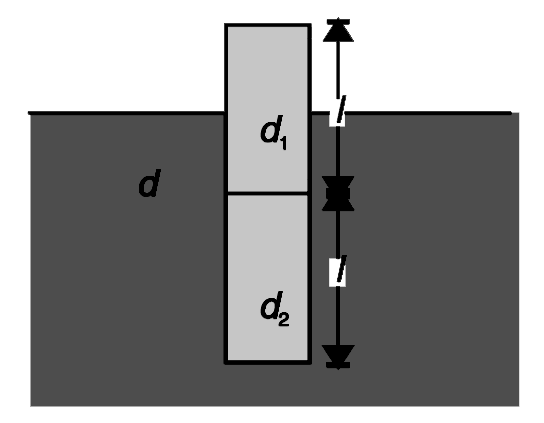
A cylindrical block of length 2l is made of two different materials. The uppwer half has density d1 and and lower half, which is heavier, has density d2 the block is floating in a liquid of unknown density d with l2 of its length outside the liquid.
(a) Find d
(b) Show that d>4d13
View SolutionA body weighs W1 in a liquid of density ρ1 and W2 in a liquid of density ρ2. What is the weight of body in a liquid of density ρ3?
View Solution
Knowledge Check
A body of density D1 and mass M is moving downward in glycerine of density D2. What is the viscous force acting on it ?
AMg(1−D2D1)BMg(1−D1D2)CMgD1DMgD2A body of density d and volume V floats with volumes V of its total volume V immersed in a liquid of density d and the rest of the volume V2 immersed in another liquid of density d2(<d1). The volume V1 immersed in liquid of density d1 is
Ad1d2VB(d1−d2d1)VC(d+d2d1+d2)VD(d−d2d1−d2)VAn object weights m1 in a liquid of density d1 and that in liquid of density d2 is m2. The density of the object is
Am2d2−m1d1m2−m1Bm1d1−m2d2m2−m1Cm2d1−m1d2m1−m2Dm1d2−m2d1m1−m2
A body of density D1 and mass M is moving downward in glycerine of density D2. What is the viscous force acting on it ?
View SolutionA body of density ρfloats with a volume V1 of its total volume V immersed in one liquid of density ρ1 and with the remainder of volume V2 immersed in another liquid of density ρ2, where ρ1>ρ2. Find the relative volumes immersed in two liquids.
View SolutionA solid of density D is floating in a liquid of density d. If V is the volume of solid submerged in the liquid and V is the total volume of the solid, then V/V is equal to
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If ρ is the surface tension the diameter of the drop of the liquid is
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If ρ is the surface tension the diameter of the drop of the liquid is
View Solution
