When a particle of mass m moves on the x-axis in a potential of the form $V (x) = k x^{2}$ it performs simple harmonic motion. The correspondubing time period is proprtional to $\frac{\sqrt{m}}{h}$ , as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of $x = 0$ in a way different from $k x^{2}$ and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is $V (x) = a x^{4} (a > 0)$ for |x| neat the origin and becomes a constant equal to $V_{0}$ for |x|impliesX_(0) (see figure).

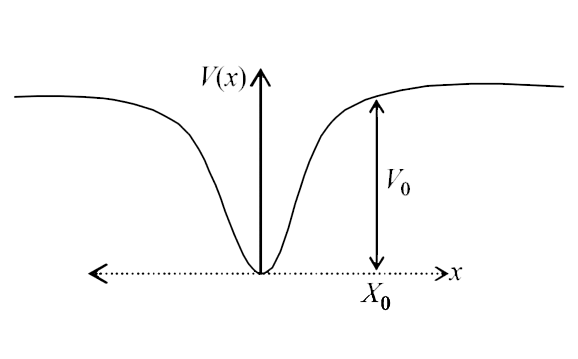
If total energy of the particle is E, it will perform perildic motion only if.

(a) $E < 0$

(b) $E > 0$

(c ) $V_{0} > E > 0$

(d) $E > V_{0}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

If the energy is zero, the particle will not perform oscillations. Therefore € should be greater than zero. Further if (c ) $E = V_{0}$ , the potential energy will become constant as depicted in the potential energy will become constant as depicted in the graph given. In this acse also the particle will not oscillate.
Therefore (E) should be than zero but less than $V_{0}$ .

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
When a particle of mass m moves on the X-axis in a potential of the form $V (x) = k x^{2}$ , it performs simple harmonic motion. The corresponding time period is proportional to
$\sqrt{\frac{m}{k}}$ , as can be seen easily using dimensional analysis.
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from $k x^{2}$ and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is V(x) $= a x^{2} (a > 0)$ for |x| near the origin and becomes a constant equal to $V_{0}$ for $| x | \geq X_{0}$

The acceleration of this particle for $| X | > X_{0}$ is
Aproportional to $(\frac{v_{0}}{m X_{0}})$
Bpropotinal to $\frac{\sqrt{V_{0}}}{m X_{0}}$
Cproportional to $V_{0}$
DZero
Question 2 - Select One
When a particle is mass $m$ moves on the $x -$ axis in a potential of the from $V (x) = k x^{2}$ , it performs simple harmonic motion. The corresponding thime periond is proportional to $\sqrt{\frac{m}{k}}$ , as can be seen easily asing dimensional analysis. However, the motion of a pariticle can be periodic even when its potential enem increases on both sides $x = 0$ in a way different from $k x^{2}$ and its total energy is such that the particel does not escape to infinity. consider a particle of mass $m$ moving onthe $x -$ axis . Its potential energy is $V (x) = α \cdot x^{4} (α > 0$ ) for $| x |$ near the origin and becomes a constant equal to $V_{0}$ for $| x | \geq X_{0}$ (see figure)

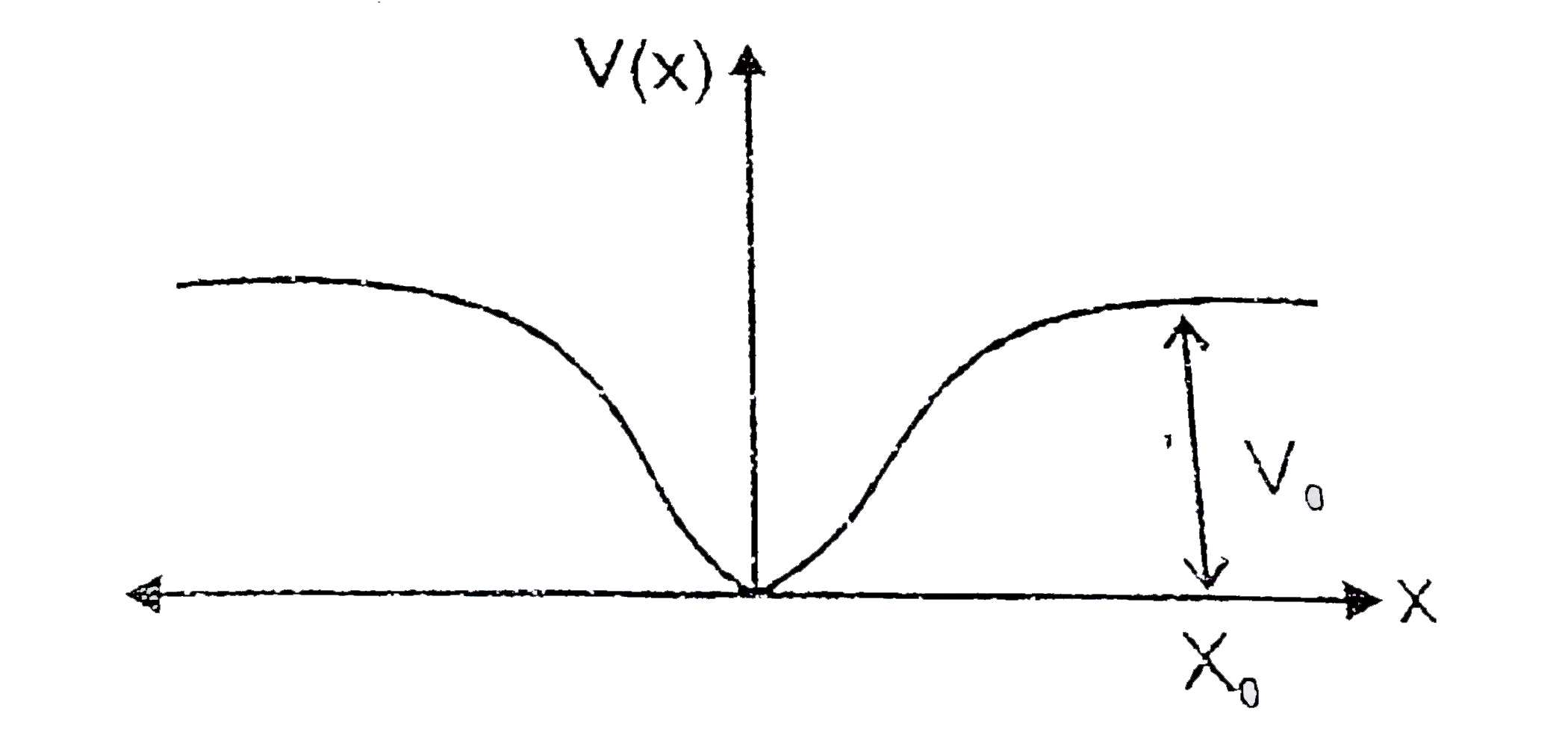
If the total energy of the particle is $E$ , it will perform is periodic motion why if :
A $E < 0$
B $E > 0$
C $V_{0} > E > 0$
D $E > V_{0}$
Question 3 - Select One
When a particle of mass m moves on the X-axis in a potential of the form $V (x) = k x^{2}$ , it performs simple harmonic motion. The corresponding time period is proportional to
$\sqrt{\frac{m}{k}}$ , as can be seen easily using dimensional analysis.
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from $k x^{2}$ and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is V(x) $= a x^{2} (a > 0)$ for |x| near the origin and becomes a constant equal to $V_{0}$ for $| x | \geq X_{0}$

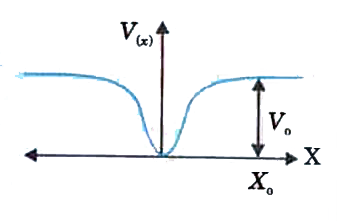
For periodic motion os small amplitude A . The time periodic T of this particle is proportional to
A $A \frac{\sqrt{m}}{α}$
B $\frac{1}{A} \frac{\sqrt{m}}{α}$
C $A \frac{\sqrt{α}}{m}$
D $\frac{1}{A} \frac{\sqrt{α}}{m}$

SUNIL BATRA (41 YEARS IITJEE PHYSICS)-SIMPLE HARMONIC MOTION-JEE Main And Advanced

Home
Ask Doubt
Profile

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

SUNIL BATRA (41 YEARS IITJEE PHYSICS)-SIMPLE HARMONIC MOTION-JEE Main And Advanced