When an inductor coil is connected to an ideal battery of emf 10V, a constant current 2.5 A flows. When the same inductor coil is connected to an ac source of 10V and 50 HZ then the current is 2A. Find out the inductance of the coil.
The correct Answer is:3/100πH
To find the inductance of the coil, we will follow these steps:
Step 1: Calculate the Resistance of the Coil
When the inductor coil is connected to a DC source (battery), we can use Ohm's law to find the resistance (R) of the coil.
Using Ohm's law:
V=I×R
Where:
- V=10V (emf of the battery)
- I=2.5A (current flowing through the coil)
Rearranging the formula to find R:
R=VI=10V2.5A=4Ω
Step 2: Calculate the Impedance of the Coil
When the same coil is connected to an AC source, we can calculate the impedance (Z) using the formula:
Z=VI
Where:
- V=10V (voltage of the AC source)
- I=2A (current flowing through the coil)
Calculating Z:
Z=10V2A=5Ω
Step 3: Relate Impedance, Resistance, and Inductive Reactance
The impedance of the coil in an AC circuit is given by:
Z=√R2+X2L
Where:
- XL is the inductive reactance.
Squaring both sides gives:
Z2=R2+X2L
Substituting the values we found:
52=42+X2L
25=16+X2L
Step 4: Solve for Inductive Reactance
Rearranging gives:
X2L=25−16=9
Taking the square root:
XL=3Ω
Step 5: Calculate the Inductance of the Coil
The inductive reactance XL is related to the inductance L and the angular frequency ω by the formula:
XL=ωL
Where:
ω=2πf
And given f=50Hz:
ω=2π×50=100π
Now substituting XL into the equation:
3=(100π)L
Rearranging to find L:
L=3100π
Final Answer
The inductance of the coil is:
L=3100πH
---
When the inductor coil is connected to a DC source (battery), we can use Ohm's law to find the resistance (R) of the coil.
V=I×R
- V=10V (emf of the battery)
- I=2.5A (current flowing through the coil)
R=VI=10V2.5A=4Ω
When the same coil is connected to an AC source, we can calculate the impedance (Z) using the formula:
Z=VI
- V=10V (voltage of the AC source)
- I=2A (current flowing through the coil)
Z=10V2A=5Ω
The impedance of the coil in an AC circuit is given by:
Z=√R2+X2L
- XL is the inductive reactance.
Z2=R2+X2L
52=42+X2L
25=16+X2L
Rearranging gives:
X2L=25−16=9
Taking the square root:
XL=3Ω
The inductive reactance XL is related to the inductance L and the angular frequency ω by the formula:
XL=ωL
ω=2πf
And given f=50Hz:
ω=2π×50=100π
3=(100π)L
L=3100π
The inductance of the coil is:
L=3100πH
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Single Correct
63 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercises Multiple Correct
5 Videos
- ALTERNATING CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise 5.1
15 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
Similar Questions
A long solenoid connected to a 12V DC source passes a steady current of 2 A. When the solenoid is connected to an AC source of 12V at 50 Hz, the current flowing is 1A. Calculate inductance of the solenoid.
View SolutionWhen a coil is connected to a 100 V D.C. supply, the current is 2 A. When the same coil is connected to A.C. source E=100√2sinωt, the current is 1 A. Find the inductive reactance used in the circuit.
View Solution(a) In a series LCR circuit connected across an AC source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with frequency of the AC source.
(b) What is the phase difference between the voltages across inductor and the capacitor at resonance in the LCR circuit ?
(c ) When and inductor is connected to a 200 V DC voltage, a current of 1Aflows trough it. when the same inductor is connected to a 200 V, 50 Hz AC source, only 0.5 A current flows. Explain, why ? Also, calculate the self inductance of the inductor.
View SolutionA bulb is conneted to an ideal battery of emf 10 V so that the resulting current is 10 mA. When the bulb is connected to 220 V mains (ideal), the current is 50 mA. Choose the correct alternative (s)
View SolutionAn ideal inductor of inductance 50μH is connected to an AC source of 220V, 50 Hz. Find the inductive reactance.
View SolutionA steady 4A flows in an inductor coil when connected to a 12V source as shown in figure. If the same coil is connected to an ac source of 12V, 50rad/s a currentd of 2.4A flows in the circuit as shown in figure2. Now after these observations , a capacitor fo capacitance 150F is connected in series with the coil and with same AC source as shown in figure 3.
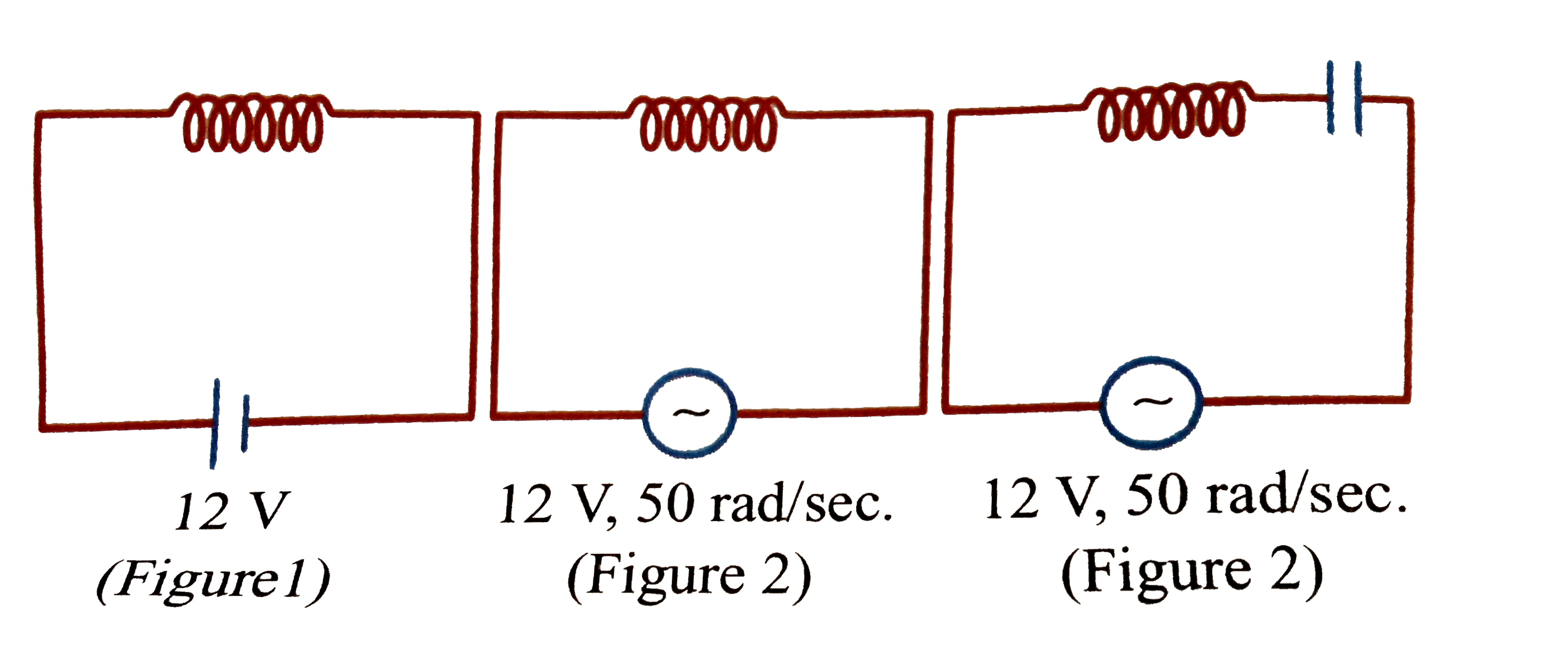
The resistance of the coil is:
View SolutionA current of 4 A flows in a coil when it is connected to a 12V dc source. When the same coil is connected to an a.c. source (12 V, 8 Hz), a current of 2.4 A flows in the coil. Calculate coefficient of self inductance (L) of the coil.
View SolutionAn inductor coil is connected to a 12V battery and drawing a current 24 A. This coil is connected to capacitor and an AC source of rms voltage rating 24 V in the series connection. The rms current through the circuit would found to be
View SolutionIn the pure inductive circuit, the curves between frequency f and reciprocal of inductive reactance 1/XL is
View SolutionA current of 6 A flows in a coil when connected to a dc source of 18 V. If the same coil is connected to an ac source of 20 V, 50 rad/s, a current of 4 A flows in the circuit. The inductance of the coil is 10x mH. Find out the value of x.
View Solution
