A current of 4 A flows in a coil when it is connected to a 12V dc source. When the same coil is connected to an a.c. source (12 V, 8 Hz), a current of 2.4 A flows in the coil. Calculate coefficient of self inductance (L) of the coil.
To solve the problem of finding the coefficient of self-inductance (L) of the coil, we will follow these steps:
Step 1: Determine the resistance (R) of the coil using the DC source.
Given:
- Voltage (E) = 12 V
- Current (I) = 4 A
Using Ohm's Law:
R=EI
R=12V4A=3Ω
Step 2: Analyze the AC circuit.
When the coil is connected to an AC source:
- Voltage (E) = 12 V
- Current (I) = 2.4 A
- Frequency (f) = 8 Hz
The relationship between voltage, current, resistance, and inductive reactance (X_L) in an AC circuit is given by:
I=E√R2+X2L
Step 3: Substitute known values into the equation.
Substituting the values we have:
2.4=12√32+X2L
Step 4: Rearrange the equation to solve for XL.
Squaring both sides:
(2.4)2=12232+X2L
5.76=1449+X2L
Cross-multiplying gives:
5.76(9+X2L)=144
51.84+5.76X2L=144
Step 5: Solve for X2L.
Rearranging gives:
5.76X2L=144−51.84
5.76X2L=92.16
X2L=92.165.76
X2L=16
XL=4Ω
Step 6: Relate inductive reactance to self-inductance (L).
Inductive reactance is given by:
XL=ωL
Where:
ω=2πf
Substituting the frequency:
ω=2π(8)=16π
Step 7: Substitute XL back into the equation.
Now we can write:
4=(16π)L
L=416π
L=14π
Step 8: Calculate the value of L.
Using π≈3.14:
L≈14×3.14
L≈112.56
L≈0.0796H
Thus, the coefficient of self-inductance L of the coil is approximately 0.080 H.
---
Given:
- Voltage (E) = 12 V
- Current (I) = 4 A
R=EI
R=12V4A=3Ω
When the coil is connected to an AC source:
- Voltage (E) = 12 V
- Current (I) = 2.4 A
- Frequency (f) = 8 Hz
I=E√R2+X2L
Substituting the values we have:
2.4=12√32+X2L
Squaring both sides:
(2.4)2=12232+X2L
5.76=1449+X2L
5.76(9+X2L)=144
51.84+5.76X2L=144
Rearranging gives:
5.76X2L=144−51.84
5.76X2L=92.16
X2L=92.165.76
X2L=16
XL=4Ω
Inductive reactance is given by:
XL=ωL
Where:
ω=2πf
Substituting the frequency:
ω=2π(8)=16π
Now we can write:
4=(16π)L
L=416π
L=14π
Using π≈3.14:
L≈14×3.14
L≈112.56
L≈0.0796H
Similar Questions
A current of 6 A flows in a coil when connected to a dc source of 18 V. If the same coil is connected to an ac source of 20 V, 50 rad/s, a current of 4 A flows in the circuit. The inductance of the coil is 10x mH. Find out the value of x.
View SolutionA current of 4A flows in a coil when connected to a 12VDC source. If the same coil is connected to a 12V,50rad/sAC source, a current of 2.4A flows in the circuit. Determine the inductance of the coil. Also, find the power developed in the circuit if a2500μF capacitor is connected in series with the coil.
View SolutionA current of 4A flows in a coil when connected to a 12VDC source. If the same coil is connected to a 12V,50rad/sAC source, a current of 2.4A flows in the circuit. Determine the inductance of the coil. Also, find the power developed in the circuit if a2500μF capacitor is connected in series with the coil.
View SolutionA current of 4A flows in a coil when connected to a 12VDC source. If the same coil is connected to a 12V,50rad/sAC source, a current of 2.4A flows in the circuit. Determine the inductance of the coil. Also, find the power developed in the circuit if a2500μF capacitor is connected in series with the coil.
View SolutionA current of 4 A flows in a coil when connected to a 12 V dc source. If the same coil is connected to a 12V,50rads−1 ac source, a current of 2.4 A flows of the coil in the circuit.
The power developed in the circuit of a 2500(μ)F capacitor that is connected in series with the coil is
View SolutionA steady 4A flows in an inductor coil when connected to a 12V source as shown in figure. If the same coil is connected to an ac source of 12V, 50rad/s a currentd of 2.4A flows in the circuit as shown in figure2. Now after these observations , a capacitor fo capacitance 150F is connected in series with the coil and with same AC source as shown in figure 3.
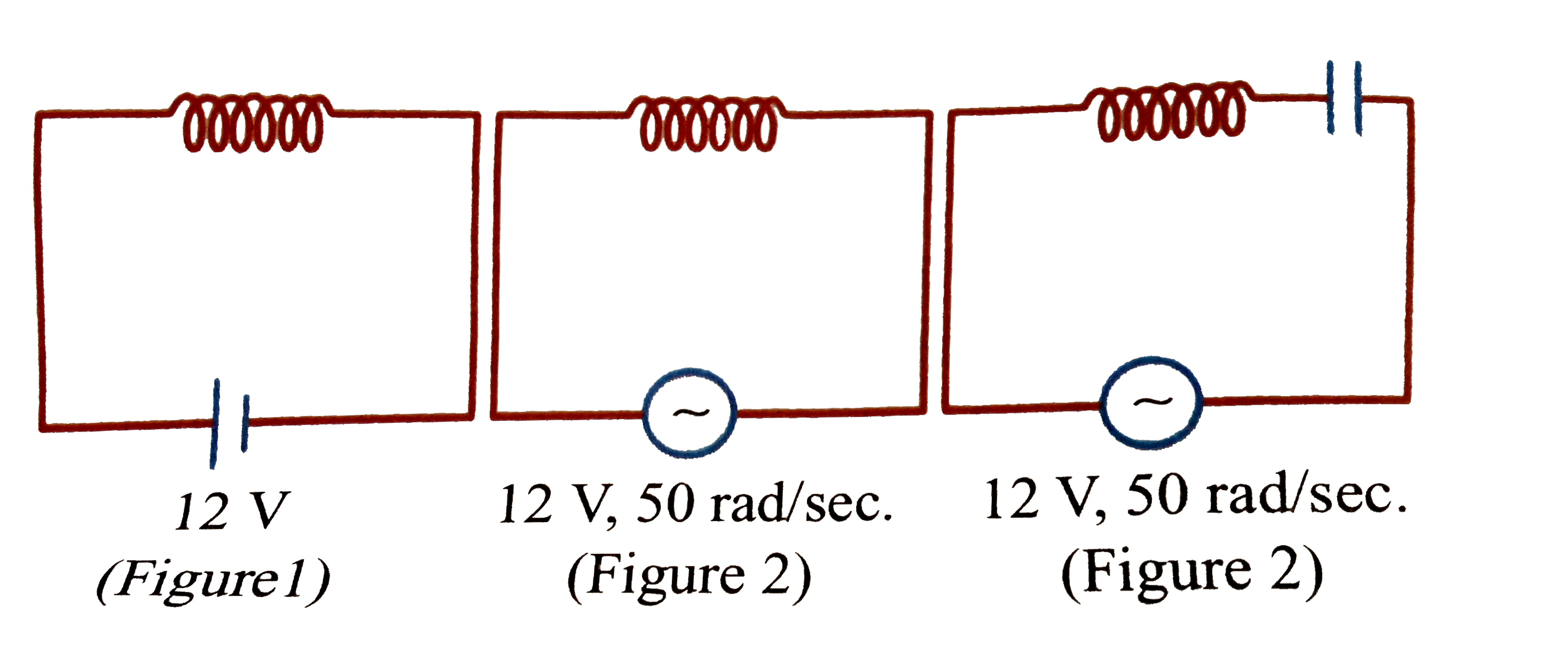
The resistance of the coil is:
View SolutionA long solenoid connected to a 12V DC source passes a steady current of 2 A. When the solenoid is connected to an AC source of 12V at 50 Hz, the current flowing is 1A. Calculate inductance of the solenoid.
View SolutionWhen a coil is connected to a 100 V D.C. supply, the current is 2 A. When the same coil is connected to A.C. source E=100√2sinωt, the current is 1 A. Find the inductive reactance used in the circuit.
View SolutionIn the pure inductive circuit, the curves between frequency f and reciprocal of inductive reactance 1/XL is
View SolutionWhen an inductor coil is connected to an ideal battery of emf 10V, a constant current 2.5 A flows. When the same inductor coil is connected to an ac source of 10V and 50 HZ then the current is 2A. Find out the inductance of the coil.
View Solution
